
科目: 来源: 题型:
【题目】已知函数f(x)=|2x﹣3|+x+1.
(1)求函数f(x)的最小值;
(2)当x≥1时,关于x的不等式f(2x)<4x+2a恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() ,
,![]() 的极坐标方程分别为
的极坐标方程分别为![]() ,
,![]() .
.
(1)将直线![]() 的参数方程化为极坐标方程,将
的参数方程化为极坐标方程,将![]() 的极坐标方程化为参数方程;
的极坐标方程化为参数方程;
(2)当![]() 时,直线
时,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生对“两个一百年”奋斗目标、实现中华民族伟大复兴中国梦的“关注度”(单位:天),某中学团委组织学生在十字路口采用随机抽样的方法抽取了80名青年学生(其中男女人数各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组青年学生的月“关注度”分为6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)现从“关注度”在![]() 的男生与女生中选取3人,设这3人来自男生的人数为
的男生与女生中选取3人,设这3人来自男生的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(3)在抽取的80名青年学生中,从月“关注度”不少于25天的人中随机抽取2人,求至少抽取到1名女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】玉山一中篮球体育测试要求学生完成“立定投篮”和“三步上篮”两项测试,“立定投篮”和“三步上篮”各有2次投篮机会,先进行“立定投篮”测试,如果合格才能参加“三步上篮”测试.为了节约时间,每项测试只需且必须投中一次即为合格.小华同学“立定投篮”和“三步上篮”的命中率均为![]() .假设小华不放弃任何一次投篮机会且每次投篮是否命中相互独立.
.假设小华不放弃任何一次投篮机会且每次投篮是否命中相互独立.
(1)求小华同学两项测试均合格的概率;
(2)设测试过程中小华投篮次数为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A、B,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )

A.y2=9xB.y2=6x
C.y2=3xD.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知五面体ABCDEF中,四边形CDEF为矩形,![]() ,CD=2DE=2AD=2AB=4,AC=
,CD=2DE=2AD=2AB=4,AC=![]() ,
,![]() .
.
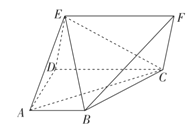
(1)求证:AB![]() 平面ADE;
平面ADE;
(2)求平面EBC与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)已知函数f(x)![]() (2x
(2x![]() ),若f(
),若f(![]() )
)![]() ,θ∈(0,
,θ∈(0,![]() ),求tanθ.
),求tanθ.
(2)若函数g(x)=﹣(![]() sin
sin![]() cos
cos![]() )cos
)cos![]() ,讨论函数g(x)在区间[
,讨论函数g(x)在区间[![]() ,
,![]() 上的单调性.
上的单调性.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系.已知曲线
轴的正半轴为极轴,建立极坐标系.已知曲线![]() :
:![]() (
(![]() 为参数),
为参数), ![]() :
:![]() (
(![]() 为参数).
为参数).
(1)化![]() ,
,![]() 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() ,
,![]() 为
为![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某地区中小学生人数和近视情况如图1和图2所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生作为样本进行调查.

(1)求样本容量和抽取的高中生近视人数分别是多少?
(2)在抽取的![]() 名高中生中,平均每天学习时间超过9小时的人数为
名高中生中,平均每天学习时间超过9小时的人数为![]() ,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
平均学习时间不超过9小时 | 平均学习时间超过9小时 | 总计 | |
不近视 | |||
近视 | |||
总计 |
(3)根据(2)中的列联表,判断是否有![]() 的把握认为高中生平均每天学习时间与近视有关?
的把握认为高中生平均每天学习时间与近视有关?
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com