
科目: 来源: 题型:
【题目】进入冬天,大气流动性变差,容易形成雾握天气,从而影响空气质量.某城市环保部门试图探究车流量与空气质量的相关性,以确定是否对车辆实施限行.为此,环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
车流量(x万辆) | 10 | 9 | 9.5 | 10.5 | 11 | 8 | 8.5 |
空气质量指数y | 78 | 76 | 77 | 79 | 80 | 73 | 75 |
(1)根据表中周一到周五的数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
附:回归方程![]() 中斜率和截距最小二乘估计公式分别为:
中斜率和截距最小二乘估计公式分别为:
 其中:
其中:![]()
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】据市场分析,广饶县驰中集团某蔬菜加工点,当月产量在10吨至25吨时,月生产总成本![]() (万元)可以看成月产量
(万元)可以看成月产量![]() (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(1)写出月总成本![]() (万元)关于月产量
(万元)关于月产量![]() (吨)的函数关系;
(吨)的函数关系;
(2)已知该产品销售价为每吨1.6万元,那么月产量为多少时,可获最大利润;
(3)当月产量为多少吨时, 每吨平均成本最低,最低成本是多少万元?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() ,三点
,三点![]() ,
,![]() ,
,![]() 中仅有一个点在抛物线
中仅有一个点在抛物线![]() 上.
上.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设直线![]() 不经过
不经过![]() 点且与
点且与![]() 相交于
相交于![]() 两点.若直线
两点.若直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,证明:
,证明:![]() 过定点.
过定点.
查看答案和解析>>
科目: 来源: 题型:
【题目】“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为8元,被随机分配为1.72元,1.83元,2.28元,1.55元,0.62元, 5份供甲、乙等5人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于3元的概率是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.右图是以往公司对该产品的宣传费用![]() (单位:万元)和产品营业额
(单位:万元)和产品营业额![]() (单位:万元)的统计折线图.
(单位:万元)的统计折线图.

(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用![]() 与产品营业额
与产品营业额![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(Ⅱ)建立产品营业额![]() 关于宣传费用
关于宣传费用![]() 的回归方程;
的回归方程;
(Ⅲ)若某段时间内产品利润![]() 与宣传费
与宣传费![]() 和营业额
和营业额![]() 的关系为
的关系为![]() 应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:相关系数 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为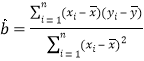 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,设点A(-3,0),B(3,0),直线AM,BM相交于点M,且它们的斜率之积是![]()
(1)试讨论点M的轨迹形状;
(2)当0<b<3时,若点M的轨迹上存在点P(P在x轴的上方),使得∠APB=120°,求b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设![]() 或
或![]() ,
,![]() ,若
,若![]() 是
是![]() 的充分条件.
的充分条件.
(1)求证:函数![]() 的图像总在直线
的图像总在直线![]() 的下方;
的下方;
(2)是否存在实数![]() ,使得不等式
,使得不等式![]() 对一切实数
对一切实数![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱台![]() 的上下底面分别是边长为2和4的正方形,
的上下底面分别是边长为2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 边上找一点
边上找一点![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖.每次抽奖都是从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com