【题目】在直角坐标系中，圆经过伸缩变换后得到曲线．以坐标原点为极点，轴的正半轴为极轴，并在两种坐标系中取相同的单位长度，建立极坐标系，直线的极坐标方程为．

（1）求曲线的直角坐标方程及直线的直角坐标方程；

（2）设点是上一动点，求点到直线的距离的最大值．

【题目】已知函数

（Ⅰ）讨论函数在上的单调性；

（Ⅱ）证明：恒成立.

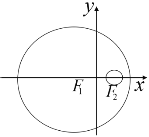
【题目】如图，已知圆的方程为，圆的方程为，若动圆与圆内切，与圆外切．

（Ⅰ）求动圆圆心的轨迹的方程；

（Ⅱ）过直线上的点作圆的两条切线，设切点分别是，，若直线与轨迹交于，两点，求的最小值．

（1）你是否能够判断年薪为9万元的员工在这家公司算高收入者？

（2）如果招聘员继续告诉你，“员工年收入的变化范围是从3万到200万”，这个信息是否足以使你作出自己是否受聘的决定？为什么？

（3）如果招聘员继续给你提供了如下信息，员工收人的第一四分位数为4.5万，第三四分位数为9.5万，你又该如何使用这条信息来作出是否受聘的决定？

（4）根据（3）中招聘员提供的信息，你能估计出这家公司员工收入的中位数是多少吗？为什么平均数比估计出的中位数高很多？

【题目】已知过抛物线的焦点，斜率为的直线交抛物线于两点，且.

(1)求该抛物线的方程；

(2) 为坐标原点，为抛物线上一点，若，求的值．

0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39 1.02

1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62 1.68

1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91 1.31

（1）请用合适的统计图描述上述数据，并分析这30条鱼的汞含量的分布特点；

（2）求出上述样本数据的平均数和标准差；

（3）从实际情况看，许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过你认为每批这种鱼的平均承含量都比1.00ppm大吗？

（4）在上述样本中，有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内？

【题目】在等差数列

（Ⅰ）求数列的通项公式；

（Ⅱ）若数列，求数列的前n项和Sn.

（Ⅰ）求证：PA∥平面BDE；

（Ⅱ）平面PAC⊥平面BDE；

（Ⅲ）若二面角E-BD-C为30°，求四棱锥P-ABCD的体积．

【题目】已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球个.若从袋子中随机抽取1个小球，取到标号为2的小球的概率是.

（1）求的值；

（2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球标号为，第二次取出的小球标号为.记“”为事件，求事件的概率.

【题目】已知双曲线具有性质：若、是双曲线左、右顶点，为双曲线上一点，且在第一象限.记直线，的斜率分别为，，那么与之积是与点位置无关的定值.

（1）试对椭圆，类比写出类似的性质（不改变原有命题的字母次序），并加以证明.

（2）若椭圆的左焦点，右准线为，在（1）的条件下，当取得最小值时，求的垂心到轴的距离.