
科目: 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=2,AA1=2![]() ,D是AA1的中点,BD与AB1交于点O,且CO⊥ABB1A1平面.
,D是AA1的中点,BD与AB1交于点O,且CO⊥ABB1A1平面.
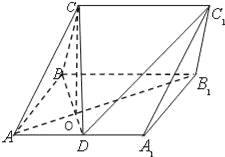
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线CD与平面ABC所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了研究学生的数学核心素养与抽象能力(指标x)、推理能力(指标y)、建模能力(指标z的相关性,将它们各自量化为1、2、3三个等级,再用综合指标w=x+y+x的值评定学生的数学核心素养,若![]() ,则数学核心素养为一级;若则数学核心素养为二级:若
,则数学核心素养为一级;若则数学核心素养为二级:若![]() ,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:
,则数学核心素养为三级,为了了解某校学生的数学核心素养,调查人员随机访问了某校10名学生,得到如下数据:

(1)在这10名学生中任取两人,求这两人的建棋能力指标相同条件下综合指标值也相同的概率;
(2)在这10名学生中任取三人,其中数学核心素养等级足一级的学生人数记为X,求随机变量X的分布列及其数学期望。
查看答案和解析>>
科目: 来源: 题型:
【题目】设△ABC三个内角A、B、C所对的边分别为![]() 已知
已知![]()
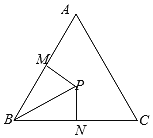
(1)求角B的大小;
(2)如图,在△ABC内取一点P,使得PB=2,过点P分别作直线BA、BC的垂线PM、PN,垂足分别是M、N,设∠PBA=![]() 求四边形PMBN的面积的最大值及此时
求四边形PMBN的面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,命题
,命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的椭圆,命题
轴上的椭圆,命题![]() 方程
方程![]() 表示双曲线.
表示双曲线.
(1)若命题![]() 是真命题,求实数
是真命题,求实数![]() 的范围;
的范围;
(2)若命题“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”是假命题,求实数
”是假命题,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列![]() 满足
满足![]() ,其中
,其中![]() ,且
,且![]() 为常数.
为常数.
(1)若![]() 是等差数列,且公差
是等差数列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且数列
,且数列![]() 满足
满足![]() 对任意的
对任意的![]() 都成立.
都成立.
①求数列![]() 的前
的前![]() 项之和
项之和![]() ;
;
②若![]() 对任意的
对任意的![]() 都成立,求
都成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.
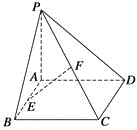
求证:(1)CD⊥PD;(2)EF⊥平面PCD.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区农产品近几年的产量统计如下表:

为了研究计算的方便,工作人员将上表的数据进行了处理,![]() 得到下表:
得到下表:

(1)根据表中数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若近几年该农产品每万吨的价格![]() (万元)与年产量
(万元)与年产量![]() (万吨)满足
(万吨)满足![]() ,且每年该农产品都能售完,当年产量
,且每年该农产品都能售完,当年产量![]() 为何值时,销售额
为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分別为:
的斜率和截距的最小二乘估计分別为: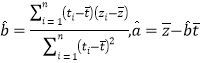 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com