
科目: 来源: 题型:
【题目】下图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.
(单位:亿元)的折线图.
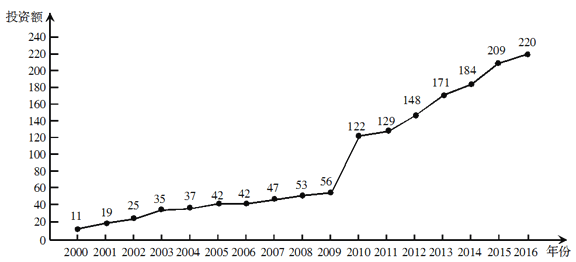
为了预测该地区2018年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型①:
)建立模型①:![]() ;根据2010年至2016年的数据(时间变量
;根据2010年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型②:
)建立模型②:![]() .
.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解甲、乙两校学生自主招生通过情况,从甲校抽取60人,从乙校抽取50人进行分析。

(1)根据题目条件完成上面2×2列联表,并据此判断是否有99%的把握认为自主招生通过情况与学生所在学校有关;
(2)现已知甲校![]() 三人在某大学自主招生中通过的概率分别为
三人在某大学自主招生中通过的概率分别为![]() ,
,![]() ,
,![]() ,用随机变量X表示
,用随机变量X表示![]() 三人在该大学自主招生中通过的人数,求X的分布列及期望
三人在该大学自主招生中通过的人数,求X的分布列及期望![]() .
.
参考公式:![]() .
.
参考数据:
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四面体ABCD中作截面PQR,若PQ与CB的延长线交于点M,RQ与DB的延长线交于点N,RP与DC的延长线交于点K.
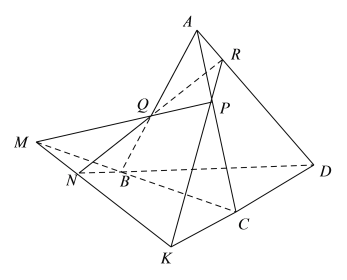
(1)求证:直线![]() 平面PQR;
平面PQR;
(2)求证:点K在直线MN上.
查看答案和解析>>
科目: 来源: 题型:
【题目】某旅行团按以下规定选择![]() 五个景区游玩:①若去
五个景区游玩:①若去![]() ,则去
,则去![]() ;②
;②![]() 不能同时去;③
不能同时去;③![]() 都去,或者都不去;④
都去,或者都不去;④![]() 去且只去一个;⑤若去
去且只去一个;⑤若去![]() ,则要去
,则要去![]() 和
和![]() .那么,这个旅游团最多能去的景区为_______.
.那么,这个旅游团最多能去的景区为_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣∞,0)∪(0,+∞),f(x)是奇函数,且当x>0时,f(x)=x2﹣x+a,若函数g(x)=f(x)﹣x的零点恰有两个,则实数a的取值范围是( )
A.a<0B.a≤0C.a≤1D.a≤0或a=1
查看答案和解析>>
科目: 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正![]() 边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出
边形求其面积,如图是其设计的一个程序框图,则框图中应填入、输出![]() 的值分别为( )
的值分别为( )
(参考数据:![]() )
)

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥![]() 中,底面 ABCD为矩形,侧面为正三角形,且平面
中,底面 ABCD为矩形,侧面为正三角形,且平面![]() 平面
平面 ![]() E 为 PD 中点,AD=2.
E 为 PD 中点,AD=2.
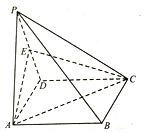
(1)证明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com