
科目: 来源: 题型:
【题目】已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系,![]() 点的极坐标为
点的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 中点
中点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,其最小正周期为
,其最小正周期为 ![]() .
.
(1)求 ![]() 的表达式;
的表达式;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后,再将得到的图象上各点的横坐标伸长到原来的
个单位长度后,再将得到的图象上各点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 ![]() 的图象,若关于
的图象,若关于 ![]() 的方程
的方程 ![]() 在区间
在区间 ![]() 上有解,求实数
上有解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】由无理数引发的数学危机一直延续到19世纪.直到1872年,德国数学家戴德金从连续性的要求出发,用有理数的“分割”来定义无理数(史称戴德金分割),并把实数理论建立在严格的科学基础上,才结束了无理数被认为“无理”的时代,也结束了持续2000多年的数学史上的第一次大危机.所谓戴德金分割,是指将有理数集![]() 划分为两个非空的子集
划分为两个非空的子集![]() 与
与![]() ,且满足
,且满足![]() ,
,![]() ,
,![]() 中的每一个元素都小于
中的每一个元素都小于![]() 中的每一个元素,则称
中的每一个元素,则称![]() 为戴德金分割.试判断,对于任一戴德金分割
为戴德金分割.试判断,对于任一戴德金分割![]() ,下列选项中,不可能成立的是()
,下列选项中,不可能成立的是()
A.![]() 没有最大元素,
没有最大元素, ![]() 有一个最小元素B.
有一个最小元素B.![]() 没有最大元素,
没有最大元素, ![]() 也没有最小元素
也没有最小元素
C.![]() 有一个最大元素,
有一个最大元素, ![]() 有一个最小元素D.
有一个最小元素D.![]() 有一个最大元素,
有一个最大元素, ![]() 没有最小元素
没有最小元素
查看答案和解析>>
科目: 来源: 题型:
【题目】设二次函数![]() 满足下列条件:当
满足下列条件:当![]() 时,
时,![]() 的最小值为0,且
的最小值为0,且![]() 成立;当
成立;当![]() 时,
时,![]() 恒成立.
恒成立.
(1)求![]() 的解析式;
的解析式;
(2)若对![]() ,不等式
,不等式![]() 恒成立、求实数
恒成立、求实数![]() 的取值范围;
的取值范围;
(3)求最大的实数![]() ,使得存在实数
,使得存在实数![]() ,只要当
,只要当![]() 时,就有
时,就有![]() 成立.
成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)从偶函数的定义出发,证明函数![]() 是偶函数的充要条件是它的图象关于y轴对称;
是偶函数的充要条件是它的图象关于y轴对称;
(2)从奇函数的定义出发,证明函数![]() 是奇函数的充要条件是它的图象关于原点对称.
是奇函数的充要条件是它的图象关于原点对称.
查看答案和解析>>
科目: 来源: 题型:
【题目】汽车急刹车的停车距离与诸多因素有关,其中最为关键的两个因素是驾驶员的反应时间和汽车行驶的速度.设d表示停车距离,![]() 表示反应距离,
表示反应距离,![]() 表示制动距离,则
表示制动距离,则![]() .下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
.下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
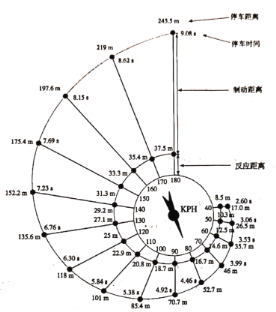
序号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格中的数据,建立停车距离与汽车速度的函数模型.可选择模型一:![]() 或模型二:
或模型二:![]() (其中v为汽车速度,a,b
(其中v为汽车速度,a,b
(2)通过计算![]() 时的停车距离,分析选择哪一个函数模型的拟合效果更好.
时的停车距离,分析选择哪一个函数模型的拟合效果更好.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年8月18日,举世瞩目的第18届亚运会在印尼首都雅加达举行,为了丰富亚运会志愿者的业余生活,同时鼓励更多的有志青年加入志愿者行列,大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛(满分120分)并计划对成绩前15名的志愿者进行奖励,现将所有志愿者的竞赛成绩制成频率分布直方图,如图所示,若第三组与第五组的频数之和是第二组的频数的3倍,试回答以下问题:
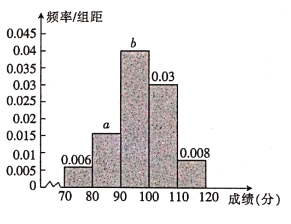
(1)求图中![]() 的值;
的值;
(2)求志愿者知识竞赛的平均成绩;
(3)从受奖励的15人中按成绩利用分层抽样抽取5人,再从抽取的5人中,随机抽取2人在主会场服务,求抽取的这2人中其中一人成绩在![]() 分的概率.
分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com