
科目: 来源: 题型:
【题目】四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC![]() 底面BCDE,BC=2,CD=
底面BCDE,BC=2,CD=![]() ,AB=AC
,AB=AC
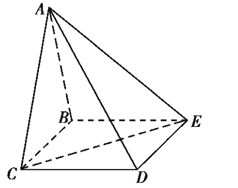
(1)证明![]() .
.
(2)设侧面ABC为等边三角形,求二面角C-AD-E的余弦值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列命题:
①线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②由变量![]() 和
和![]() 的数据得到其回归直线方程
的数据得到其回归直线方程![]() ,则
,则![]() 一定经过点
一定经过点![]() ;
;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
④将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
⑤在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.1个单位,
平均增加0.1个单位,
其中真命题的序号是_________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在以下命题中:
①三个非零向量![]() ,
,![]() ,
,![]() 不能构成空间的一个基底,则
不能构成空间的一个基底,则![]() ,
,![]() ,
,![]() 共面;
共面;
②若两个非零向量![]() ,
,![]() 与任何一个向量都不能构成空间的一个基底,则
与任何一个向量都不能构成空间的一个基底,则![]() ,
,![]() 共线;
共线;
③对空间任意一点![]() 和不共线的三点
和不共线的三点![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 四点共面
四点共面
④若![]() ,
,![]() 是两个不共线的向量,且
是两个不共线的向量,且![]() ,则
,则![]() 构成空间的一个基底
构成空间的一个基底
⑤若![]() 为空间的一个基底,则
为空间的一个基底,则![]() 构成空间的另一个基底;
构成空间的另一个基底;
其中真命题的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】给出如下四个命题:
①“![]() ”是“
”是“![]() ”的充分而不必要条件;
”的充分而不必要条件;
②命题“若![]() ,则函数
,则函数![]() 有一个零点”的逆命题为真命题;
有一个零点”的逆命题为真命题;
③若![]() 是
是![]() 的必要条件,则
的必要条件,则![]() 是
是![]() 的充分条件;
的充分条件;
④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的既不充分也不必要条件.
”的既不充分也不必要条件.
其中正确的命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】新型冠状病毒肺炎疫情爆发以来,疫情防控牵挂着所有人的心. 某市积极响应上级部门的号召,通过沿街电子屏、微信公众号等各种渠道对此战“疫”进行了持续、深入的悬窗,帮助全体市民深入了解新冠状病毒,增强战胜疫情的信心. 为了检验大家对新冠状病毒及防控知识的了解程度,该市推出了相关的知识问卷,随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
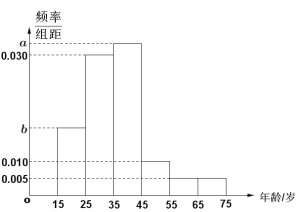
(1)求图中![]() 的值;
的值;
(2)现采取分层抽样在![]() 和
和![]() 中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的2×2列联表,并根据统计结果判断:能够有99.9%的把握认为“中老年人”比“青少年人”更加了解防控的相关知识?
了解全面 | 了解不全面 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
附表及公式: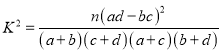 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分12分)
2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

表1:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 4 | 36 | 96 | 28 | 32 | 4 |
(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据图1和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)根据市场调查,设备改造后,每生产一件合格品企业可获利180元,一件不合格品亏损 100元,用频率估计概率,则生产1000件产品企业大约能获利多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() 经过原点
经过原点![]() 且与直线
且与直线![]() 相切于点
相切于点![]()
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)在圆![]() 上是否存在两点
上是否存在两点![]() 关于直线
关于直线![]() 对称,且以线段
对称,且以线段![]() 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线![]() 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com