①平面MENF⊥平面BDD′B′；

②直线AC∥平面MENF始终成立；

③四边形MENF周长L＝f(x)，x∈[0,1]是单调函数；

④四棱锥C′－MENF的体积V＝h(x)为常数；

以上结论正确的是__________．

【题目】已知数列满足对时，，其对，有，则数列的前50项的和为__________．

【题目】已知函数，点在曲线上，且曲线在点处的切线与直线垂直．

（1）求，的值；

（2）如果当时，都有，求的取值范围．

【题目】已知抛物线的顶点为原点，其焦点到直线的距离为．设为直线上的点，过点作抛物线的两条切线，其中为切点．

(1) 求抛物线的方程；

(2) 当点为直线上的定点时，求直线的方程；

(3) 当点在直线上移动时，求的最小值．

【题目】某厂家举行大型的促销活动，经测算，当某产品促销费用为x（万元）时，销售量t（万件）满足（其中，）．现假定产量与销售量相等，已知生产该产品t万件还需投入成本万元（不含促销费用），产品的销售价格定为元/件．

（1）将该产品的利润y（万元）表示为促销费用x（万元）的函数；

（2）促销费用投入多少万元时，厂家的利润最大．

【题目】2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，造成165.17万人受灾，5.6万人紧急转移安置，288间房屋倒塌，46.5千公顷农田受灾，直接经济损失12.99亿元．距离陆丰市222千米的梅州也受到了台风的影响，适逢暑假，小明调查了梅州某小区的50户居民由于台风造成的经济损失，将收集的数据分成，，，，五组，并作出如图频率分布直方图：

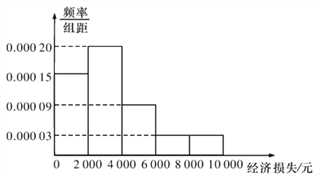
（1）试根据频率分布直方图估计小区平均每户居民的平均损失（同一组中的数据用该组区间的中点值代表）；

（2）小明向班级同学发出倡议，为该小区居民捐款，现从损失超过4000元的居民中随机抽取2户进行捐款援助，设抽出损失超过8000元的居民为户，求的分布列和数学期望；

（3）台风后区委会号召小区居民为台风重灾区捐款，小明调查的50户居民捐款情况如图，根据图表格中所给数据，分别求，，，，，，的值，并说明是否有以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？

附：临界值表参考公式：，．

(1)当b>时，判断函数f(x)在定义域上的单调性；

(2)若函数f(x)有极值点，求b的取值范围及f(x)的极值点．

【题目】如图，在多面体中，四边形为矩形，，均为等边三角形，，．

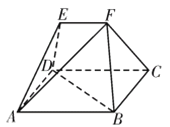
（1）过作截面与线段交于点，使得平面，试确定点的位置，并予以证明；

（2）在（1）的条件下，求直线与平面所成角的正弦值．

【题目】设函数， ．

（1）求的单调区间和极值；

（2）证明：若存在零点，则在区间上仅有一个零点．

两县城A和B相聚20km，现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为x km，建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k ,当垃圾处理厂建在的中点时，对称A和城B的总影响度为0.0065.（1）将y表示成x的函数；（11）讨论（1）中函数的单调性，并判断弧上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到城A的距离，若不存在，说明理由。