
科目: 来源: 题型:
【题目】在一次“汉马”(武汉马拉松比赛的简称)全程比赛中,50名参赛选手(24名男选手和26名女选手)的成绩(单位:分钟)分别为数据![]() (成绩不为0).
(成绩不为0).
(Ⅰ)24名男选手成绩的茎叶图如图⑴所示,若将男选手成绩由好到差编为1~24号,再用系统抽样方法从中抽取6人,求其中成绩在区间![]() 上的选手人数;
上的选手人数;

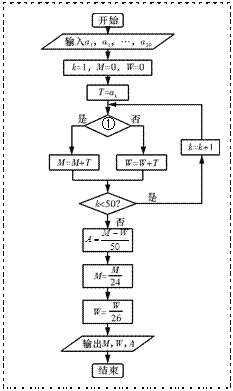
(Ⅱ)如图⑵所示的程序用来对这50名选手的成绩进行统计.为了便于区别性别,输入时,男选手的成绩数据用正数,女选手的成绩数据用其相反数(负数),请完成图⑵中空白的判断框①处的填写,并说明输出数值![]() 和
和![]() 的统计意义.
的统计意义.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018 年1月16日,由新华网和中国财经领袖联盟联合主办的2017中国财经年度人物评选结果揭晓,某知名网站财经频道为了解公众对这些年度人物是否了解,利用网络平台进行了调查,并从参与调查者中随机选出![]() 人,把这
人,把这![]() 人分为
人分为![]() 两类(
两类(![]() 类表示对这些年度人物比较了解,
类表示对这些年度人物比较了解,![]() 类表示对这些年度人物不太了解),并制成如下表格:
类表示对这些年度人物不太了解),并制成如下表格:
年龄段 |
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
(1)若按照年龄段进行分层抽样,从这![]() 人中选出
人中选出![]() 人进行访谈,并从这
人进行访谈,并从这![]() 人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在
人中随机选出两名幸运者给予奖励.求其中一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间,另一名幸运者的年龄在
岁之间,另一名幸运者的年龄在![]() 岁~
岁~![]() 岁之间的概率;(注:从
岁之间的概率;(注:从![]() 人中随机选出
人中随机选出![]() 人,共有
人,共有![]() 种不同选法)
种不同选法)
(2)如果把年龄在![]() 岁~
岁~![]() 岁之间的人称为青少年,年龄在
岁之间的人称为青少年,年龄在![]() 岁~
岁~![]() 岁之间的人称为中老年,则能否在犯错误的概率不超过
岁之间的人称为中老年,则能否在犯错误的概率不超过![]() 的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
的前提下认为青少年与中老年人在对财经年度人物的了解程度上有差异?
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知{an}是等差数列,设数列{bn}的前n项和为Sn,且2bn=b1(1+Sn),bn≠0,又a2b2=4,a7+b3=11.
(1)求{an}和{bn}的通项公式;
(2)令cn=anbn(n∈N*),求{cn}的前n项和Tn
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费对年销售量(单位:t)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费x(万元)和年销售量y(单位:t)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.

(1)根据表中数据建立年销售量y关于年宣传费x的回归方程;
(2)已知这种产品的年利润z与x,y的关系为![]() ,根据(1)中的结果回答下列问题:
,根据(1)中的结果回答下列问题:
①当年宣传费为10万元时,年销售量及年利润的预报值是多少?
②估算该公司应该投入多少宣传费,才能使得年利润与年宣传费的比值最大.
附:回归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为

参考数据:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100)六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:

(1)求第四组的频率,并补全这个频率分布直方图;
(2)请根据频率分布直方图,估计样本的众数、中位数和平均数.(每组数据以区间的中点值为代表)
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,若直线l与曲线C相交于A,B两点,求△AOB的面积.
,若直线l与曲线C相交于A,B两点,求△AOB的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)求函数![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .(Ⅱ)当
.(Ⅱ)当![]() 时,
时, ![]()
![]() ;当
;当![]() 时,
时, ![]()
![]() .
.
【解析】【试题分析】(I)利用![]() 的二阶导数来研究求得函数
的二阶导数来研究求得函数![]() 的单调区间.(II) 由(Ⅰ)得
的单调区间.(II) 由(Ⅰ)得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,由此可知
上单调递增,由此可知![]() .利用导数和对
.利用导数和对![]() 分类讨论求得函数在
分类讨论求得函数在![]() 不同取值时的最大值.
不同取值时的最大值.
【试题解析】
(Ⅰ)![]() ,
,
设![]()
![]() ,则
,则![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增,
从而得![]() 在
在![]() 上单调递增,又∵
上单调递增,又∵![]() ,
,
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
因此, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(Ⅱ)由(Ⅰ)得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
由此可知![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
设![]() ,
,
则![]()
![]()
 .
.
∵当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
①当![]() 时,
时, ![]() ,即
,即![]() ,这时,
,这时, ![]()
![]() ;
;
②当![]() 时,
时, ![]() ,即
,即![]() ,这时,
,这时, ![]()
![]() .
.
综上, ![]() 在
在![]() 上的最大值为:当
上的最大值为:当![]() 时,
时, ![]()
![]() ;
;
当![]() 时,
时, ![]()
![]() .
.
[点睛]本小题主要考查函数的单调性,考查利用导数求最大值. 与函数零点有关的参数范围问题,往往利用导数研究函数的单调区间和极值点,并结合特殊点,从而判断函数的大致图像,讨论其图象与![]() 轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.
轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.
【题型】解答题
【结束】
22
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() . 在以坐标原点为极点,
. 在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ) 写出圆 ![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
( Ⅱ ) 设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() 为圆
为圆![]() 上的任意一点,求
上的任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com