
科目: 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的最小整数N:N>100且该数列的前N项和为2的整数幂.那么该款软件的激活码是
A. 440B. 330
C. 220D. 110
查看答案和解析>>
科目: 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,线性回归模型的残差平方和
,线性回归模型的残差平方和![]() ,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
,e8.0605≈3167,其中xi, yi分别为观测数据中的温度和产卵数,i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型,求y关于x的回归方程![]() =
=![]() x+
x+![]() (精确到0.1);
(精确到0.1);
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为![]() =0.06e0.2303x,且相关指数R2=0.9522.
=0.06e0.2303x,且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比,用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线![]() =
=![]() x+
x+![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为

![]() =
=![]()
![]() ;相关指数R2=
;相关指数R2= .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】按文献记载,《百家姓》成文于北宋初年,表1记录了《百家姓》开头的24大姓氏:
表1:
赵 | 钱 | 孙 | 李 | 周 | 吴 | 郑 | 王 | 冯 | 陈 | 褚 | 卫 |
蒋 | 沈 | 韩 | 杨 | 朱 | 秦 | 尤 | 许 | 何 | 吕 | 施 | 张 |
表2记录了2018年中国人口最多的前10大姓氏:
表2:
1:李 | 2:王 | 3:张 | 4:刘 | 5:陈 |
6:杨 | 7:赵 | 8:黄 | 9:周 | 10:吴 |
从《百家姓》开头的24大姓氏中随机选取1个姓氏,则这个姓氏是2018年中国人口最多的前10大姓氏的概率为_____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的图象为不间断的曲线,定义域为
的图象为不间断的曲线,定义域为![]() ,规定:
,规定:
①如果对于任意![]() ,
,![]() 都有
都有![]() ,则称函数
,则称函数![]() 是凹函数.
是凹函数.
②如果对于任意![]() ,
,![]() 都有
都有![]() ,则称函数
,则称函数![]() 是凸函数.
是凸函数.
(1)若函数![]() (
(![]() 且
且![]() )是凹函数,试写出实数
)是凹函数,试写出实数![]() 的取值范围;(直接写出结果,无需证明);
的取值范围;(直接写出结果,无需证明);
(2)判断函数![]() 是凹函数还是凸函数,并加以证明;
是凹函数还是凸函数,并加以证明;
(3)若对任意的![]() 且
且![]() ,
,![]() ,试证明存在
,试证明存在![]() ,使
,使![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图,根据该折线图,下列结论错误的是( )
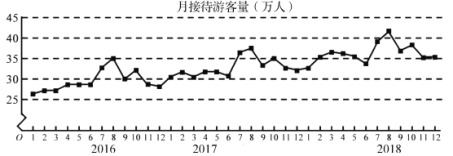
A.各年的月接待游客量高峰期大致在7,8月份
B.年接待游客量逐年增加
C.月接待游客量逐月增加
D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目: 来源: 题型:
【题目】销售甲乙两种商品所得利润分别是![]() (单位:万元)和
(单位:万元)和![]() (单位:万元),它们与投入资金
(单位:万元),它们与投入资金![]() (单位:万元)的关系有经验公式
(单位:万元)的关系有经验公式![]() ,
,![]() .今将10万元资金投入经营甲乙两种商品,其中对甲种商品投资
.今将10万元资金投入经营甲乙两种商品,其中对甲种商品投资![]() (单位:万元).
(单位:万元).
(1)试建立总利润![]() (单位:万元)关于
(单位:万元)关于![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)如何投资经营甲乙两种商品,才能使得总利润最大,并求出最大总利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com