（1）求角A的大小；

（2）若△ABC的面积S=5，b=5，求sinBsinC的值．

【题目】设是两条不同的直线，是两个不同的平面，有下列正确命题的序号是________．

(1)若m∥,n∥,则m∥n， (2)若则

(3)若，且，则； (4)若，，则

【题目】已知正项数列的首项，前n项和满足．

（1）求数列的通项公式；

（2）若数列是公比为4的等比数列，且，，也是等比数列，若数列单调递增，求实数的取值范围；

（3）若数列、都是等比数列，且满足，试证明: 数列中只存在三项．

【题目】已知函数在其定义域内有两个不同的极值点.

（1）求的取值范围；

（2）试比较与的大小，并说明理由；

（3）设的两个极值点为，证明.

【题目】某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间，需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：

以最高气温位于各区间的频率估计最高气温位于该区间的概率.

（1）求六月份这种酸奶一天的需求量（单位：瓶）的分布列；

（2）设六月份一天销售这种酸奶的利润为（单位：元），当六月份这种酸奶一天的进货量（单位：瓶）为多少时，的数学期望达到最大值？

A.（﹣3，2）B.[﹣3，2]C.（﹣2，1）D.[﹣2，1]

【题目】已知.

（1）讨论的单调性；

（2）若，且在区间上的最小值为，求的值.

【题目】（本小题满分12分）

已知抛物线C的方程C：y2="2" p x（p＞0）过点A（1，-2）.

（I）求抛物线C的方程，并求其准线方程；

（II）是否存在平行于OA（O为坐标原点）的直线l，使得直线l与抛物线C有公共点，且直线OA与l的距离等于？若存在，求出直线l的方程；若不存在，说明理由。

【答案】（I）抛物线C的方程为，其准线方程为（II）符合题意的直线l 存在，其方程为2x+y-1 =0.

【解析】

试题（Ⅰ）求抛物线标准方程，一般利用待定系数法，只需一个独立条件确定p的值：（－2）2＝2p·1，所以p＝2．再由抛物线方程确定其准线方程：，（Ⅱ）由题意设：，先由直线OA与的距离等于根据两条平行线距离公式得：解得，再根据直线与抛物线C有公共点确定

试题解析：解 （1）将（1，－2）代入y2＝2px，得（－2）2＝2p·1，

所以p＝2．

故所求的抛物线C的方程为

其准线方程为．

（2）假设存在符合题意的直线，

其方程为．

由得．

因为直线与抛物线C有公共点，

所以Δ＝4＋8t≥0，解得．

另一方面，由直线OA到的距离

可得，解得．

因为－1[－，＋∞），1∈[－，＋∞），

所以符合题意的直线存在，其方程为．

考点：抛物线方程，直线与抛物线位置关系

【名师点睛】求抛物线的标准方程的方法及流程

（1）方法：求抛物线的标准方程常用待定系数法，因为未知数只有p，所以只需一个条件确定p值即可．

（2）流程：因为抛物线方程有四种标准形式，因此求抛物线方程时，需先定位，再定量．

提醒：求标准方程要先确定形式，必要时要进行分类讨论，标准方程有时可设为y2=mx或x2=my（m≠0）．

【题型】解答题
【结束】
22

【题目】已知椭圆：的左右焦点与其短轴的一个端点是正三角形的三个顶点，点在椭圆上.

（1）求椭圆的方程；

（2）直线过椭圆左焦点交椭圆于，为椭圆短轴的上顶点，当直线时，求的面积.

【题目】为了适应高考改革，某中学推行“创新课堂”教学。高一平行甲班采用“传统教学”的教学方式授课，高一平行乙班采用“创新课堂”的教学方式授课，为了比较教学效果，期中考试后，分别从两个班中各随机抽取名学生的成绩进行统计分析，结果如下表：（记成绩不低于分者为“成绩优秀”）

（1）由以上统计数据填写下面的列联表，并判断是否有以上的把握认为“成绩优秀与教学方式有关”？

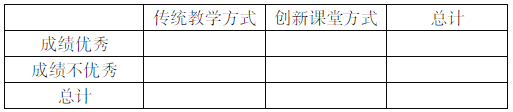
（2）现从上述样本“成绩不优秀”的学生中，抽取3人进行考核，记“成绩不优秀”的乙班人数为，求的分布列和期望.

参考公式

临界值表

A.B.C.D.