
科目: 来源: 题型:
【题目】①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②运动会的工作人员为参加![]() 接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
A.分层抽样、分层抽样、简单随机抽样B.系统抽样、简单随机抽样、分层抽样
C.简单随机抽样、简单随机抽样、分层抽样D.系统抽样、分层抽样、简单随机抽样
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四棱锥S—ABCD中,∠SDA=2∠SAD=90°,∠BAD+∠ADC=180°,AB=![]() CD,点F是线段
CD,点F是线段
SA上靠近点A的一个三等分点,AC与BD相交于E.

(1)在线段SB上作出点G,使得平面EFG∥平面SCD,请指明点G的具体位置,并用阴影部分表示平面EFG,不必说明平面EFG∥平面SCD的理由;
(2)若SA=SB=2,AB=AD=BD=![]() ,求点F到平面SCD的距离.
,求点F到平面SCD的距离.
查看答案和解析>>
科目: 来源: 题型:
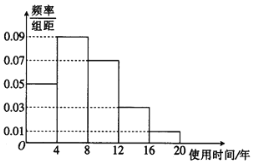
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:
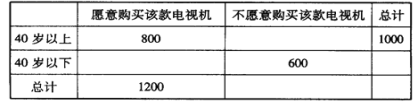
并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在[0,4)和[4,20]的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在[4,20]内的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为∠CBB1=60°的菱形,AB=AC1 .

(1)证明:平面AB1C⊥平面BB1C1C
(2)若AB⊥B1C,直线AB与平面BB1C1C所成的角为30°,求直线AB1与平面A1B1C 所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】小王投资1万元2万元、3万元获得的收益分别是4万元、9万元、16万元为了预测投资资金x(万元)与收益y万元)之间的关系,小王选择了甲模型![]() 和乙模型
和乙模型![]() .
.
(1)根据小王选择的甲、乙两个模型,求实数a,b,c,p,q,r的值
(2)若小王投资4万元,获得收益是25.2万元,请问选择哪个模型较好?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中e为自然对数的底数,m、n为常数),函数
(其中e为自然对数的底数,m、n为常数),函数![]() 定义为:对每一个给定的实数x,
定义为:对每一个给定的实数x,
(1)当m、n满足什么条件时,![]() 对所有的实数x恒成立;
对所有的实数x恒成立;
(2)设a、b是两个实数,满足![]() 且m,
且m,![]() 当
当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间
的上的单调增区间的长度之和(用含a、b的式子表示)(闭区间![]() 的长度定义为
的长度定义为![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com