假设同一公司的“骑手”一日送餐单数相同，现从两家公司各随机抽取一名“骑手”并记录其100天的送餐单数，得到如下条形图：

（Ⅰ）求乙公司的“骑手”一日工资y（单位：元）与送餐单数n（n∈N﹡）的函数关系；

（Ⅱ）若将频率视为概率，回答以下问题：

（i）记乙公司的“骑手”日工资为X（单位：元），求X的分布列和数学期望；

（ⅱ）小明拟到这两家公司中的一家应聘“骑手”的工作，如果仅从日工资的角度考虑，请你利用所学的统计学知识为他做出选择，并说明理由．

（Ⅰ）求证：平面PBC⊥平面PEB；

（Ⅱ）求平面PEB与平面PDC所成的锐二面角的余弦值．

文、理考生中分别抽取20份和50份数学试卷，进行成绩分析，

得到下面的成绩频数分布表：

（1）估计文科数学平均分及理科考生的及格人数（90分为及格分数线）；

（2）在试卷分析中，发现概念性失分非常严重，统计结果如下：

问是否有90%的把握认为概念失分与文、理考生的不同有关？（本题可以参考独立性检验临界值表：）

参考公式： ，其中.

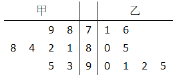
（Ⅰ）分别估计甲、乙两名同学在培训期间所有测试成绩的平均分；

（Ⅱ）从上图中甲、乙两名同学高于85分的成绩中各选一个成绩作为参考，求甲、乙两人成绩都在90分以上的概率；

（Ⅲ）现要从甲、乙中选派一人参加正式比赛，根据所抽取的两组数据分析，你认为选派哪位同学参加较为合适？说明理由.

【题目】我国南北朝时期的数学家祖暅提出体积的计算原理（祖暅原理）：“幂势既同，则积不容异”，“势”即是高，“幂”是面积．意思是：如果两等高的几何体在同高处所截得两几何体的截面积恒等，那么这两个几何体的体积相等．已知焦点在x轴上的双曲线C的离心率e＝，焦点到其渐近线的距离为2．直线y＝0与y＝2在第一象限内与双曲线C及其渐近线围成如图所示的图形OABN，则它绕y轴旋转一圈所得几何体的体积为___________．

【题目】已知函数f（x）＝（k＋）lnx＋，k∈[4，＋∞），曲线y＝f（x）上总存在两点M（x1，y1），N（x2，y2），使曲线y＝f（x）在M，N两点处的切线互相平行，则x1＋x2的取值范围为

A. （，＋∞） B. （，＋∞） C. [，＋∞） D. [，＋∞）

【题目】将函数y＝sin2x－cos2x的图象向左平移m（m＞0）个单位以后得到的图象与函数y＝ksinxcosx（k＞0）的图象关于（，0）对称，则k＋m的最小正值是

A. 2＋ B. 2＋ C. 2＋ D. 2＋

【题目】在直角坐标系中，直线的参数方程为（为参数，），以坐标原点为极点，以轴的非负半轴为极轴，建立极坐标系，曲线的极坐标方程为，已知直线与曲线交于不同的两点，.

（1）求直线的普通方程和曲线的直角坐标方程；

（2）设，求的取值范围.

【题目】已知函数对一切实数，都有成立，且.

（1）求的值；

（2）求的解析式；

（3）已知，设：当时，不等式恒成立；：当时，是单调函数.如果满足成立的的集合记为，满足成立的的集合记为，求（为全集）.

【题目】已知空间四边形ABCD，∠BAC＝，AB＝AC＝2，BD＝CD＝6，且平面ABC⊥平面BCD，则空间四边形ABCD的外接球的表面积为( )

A. 60π B. 36π C. 24π D. 12π