
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 ,其中
,其中![]() 为参数,在以坐标原点
为参数,在以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() , 直线
, 直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() ,左顶点为
,左顶点为![]() ,上顶点为
,上顶点为![]() ,
, ![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,
, ![]() 是线段
是线段![]() 的中点.若经过点
的中点.若经过点![]() 的直线
的直线![]() 与直线
与直线![]() 垂直于点
垂直于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
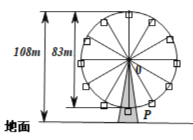
【题目】幻彩摩天轮位于中山市西区兴中广场C段4层高的建筑之上,与中山市第一家四星级酒店——富华酒店隔河相望,其外观是参考世界最高的摩天轮新加坡“飞行者”的设计,轮体上有36个吊舱,共可同时承载288人从高空俯瞰岐江一河两岸的美景.幻彩摩天轮直径为83m,每20min转一圈,最高点离地108m,摩天轮上的点P的起始位置在最低点处.已知在时刻t(min)时P距离地面的高度![]() ,(其中
,(其中![]() ),
),
(1)求![]() 的函数解析式.
的函数解析式.
(2)当离地面![]() m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆M: ![]() ,直线l:
,直线l:![]() ,下面五个命题,其中正确的是( )
,下面五个命题,其中正确的是( )
A.对任意实数k与θ,直线l和圆M有公共点;
B.对任意实数k与θ,直线l与圆M都相离;
C.存在实数k与θ,直线l和圆M相离;
D.对任意实数k,必存在实数θ,使得直线l与圆M相切:
E.对任意实数θ,必存在实数k,使得直线l与圆M相切;
查看答案和解析>>
科目: 来源: 题型:
【题目】假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程![]() 的回归系数a,b;
的回归系数a,b;
(3)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】5G网络是第五代移动通信网络,其峰值理论传输速度可达每8秒1GB,比4G网络的传输速度快数百倍.举例来说,一部1G的电影可在8秒之内下载完成.随着5G技术的诞生,用智能终端分享3D电影、游戏以及超高画质(UHD)节目的时代正向我们走来.某手机网络研发公司成立一个专业技术研发团队解决各种技术问题,其中有数学专业毕业,物理专业毕业,其它专业毕业的各类研发人员共计1200人.现在公司为提高研发水平,采用分层抽样抽取400人按分数对工作成绩进行考核,并整理得如上频率分布直方图(每组的频率视为概率).

(1)从总体的1200名学生中随机抽取1人,估计其分数小于50的概率;
(2)研发公司决定对达到某分数以上的研发人员进行奖励,要求奖励研发人员的人数达到30%,请你估计这个分数的值;
(3)已知样本中有三分之二的数学专业毕业的研发人员分数不低于70分,样本中不低于70分的数学专业毕业的研发人员人数与物理及其它专业毕业的研发人员的人数和相等,估计总体中数学专业毕业的研发人员的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在“应用![]() ”的用户中随机抽取了100名用户进行调查得到如下数据:
”的用户中随机抽取了100名用户进行调查得到如下数据:
每周使用时间 |
|
|
|
|
|
|
男 | 4 | 3 | 3 | 7 | 6 | 30 |
女 | 6 | 5 | 4 | 4 | 8 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用该“应用![]() ”时间不超过
”时间不超过![]() 的样本中,按性别分层抽样,随机抽取5名用户:
的样本中,按性别分层抽样,随机抽取5名用户:
①求抽取的5名用户中男,女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户均为男用户的概率.
(2)如果每周使用该“应用![]() ”超过
”超过![]() 的用户认为“喜欢该应用”,能否在犯错误的概率不超过0.05的前提下认为“喜欢该应用”与性别有关.
的用户认为“喜欢该应用”,能否在犯错误的概率不超过0.05的前提下认为“喜欢该应用”与性别有关.
参考公式: ,其中
,其中![]()
下面的临界值表仅供参考:
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() 的上顶点为
的上顶点为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程及其离心率;
的方程及其离心率;
(2)斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两个不同的点,当直线
两个不同的点,当直线![]() 的斜率之积是不为0的定值时,求此时
的斜率之积是不为0的定值时,求此时![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com