【题目】已知函数的图象与x轴交点为，与此交点距离最小的最高点坐标为.

（Ⅰ）求函数的表达式；

（Ⅱ）若函数满足方程，求方程在内的所有实数根之和；

（Ⅲ）把函数的图像的周期扩大为原来的两倍，然后向右平移个单位，再把纵坐标伸长为原来的两倍，最后向上平移一个单位得到函数的图像．若对任意的，方程在区间上至多有一个解，求正数k的取值范围.

【题目】随着互联网技术的快速发展，人们更加关注如何高效地获取有价值的信息，网络知识付费近两年呈现出爆发式的增长，为了了解网民对网络知识付费的态度，某网站随机抽查了岁及以上不足岁的网民共人，调查结果如下：

（1）请完成上面的列联表，并判断在犯错误的概率不超过的前提下，能否认为网民对网络知识付费的态度与年龄有关？

（2）在上述样本中用分层抽样的方法，从支持和反对网络知识付费的两组网民中抽取名，若在上述名网民中随机选人，求至少1人支持网络知识付费的概率.

附：，.

【题目】已知函数.

（1）当时，求函数在上的最小值和最大值；

（2）当时，讨论函数的单调性.

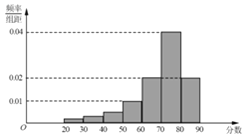
（1）从总体的1200名学生中随机抽取1人，估计其分数小于50的概率；

（2）研发公司决定对达到某分数以上的研发人员进行奖励，要求奖励研发人员的人数达到30%，请你估计这个分数的值；

（3）已知样本中有三分之二的数学专业毕业的研发人员分数不低于70分，样本中不低于70分的数学专业毕业的研发人员人数与物理及其它专业毕业的研发人员的人数和相等，估计总体中数学专业毕业的研发人员的人数．

【题目】若．

（1）讨论的单调性；

（2）若对任意，关于的不等式在区间上恒成立，求实数的取值范围．

【题目】四棱锥中，底面是中心为的菱形，，．

（1）求证：平面；

（2）若直线与平面所成的角为，求二面角正弦值．

（1）把上表补充完整，并判断能否在犯错误的概率不超过0.05的前提下认为性别与关注点高低有关？

（2）现要从上述男性用户中随机选出3名参加一项活动，以表示选中的男性用户中抢红包总次数超过10次的人数，求随机变量的分布列及数学期望．

下面的临界值表供参考：

独立性检验统计量，其中．

【题目】如图，D是AC的中点，四边形BDEF是菱形，平面平面ABC，，，．

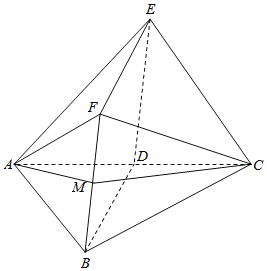
若点M是线段BF的中点，证明：平面AMC；

求平面AEF与平面BCF所成的锐二面角的余弦值．

【题目】已知圆C: ，直线l过点.

（1）若直线l与圆心C的距离为1，求直线l的方程；

（2）若直线l与圆C交于M，N两点，且，求以MN为直径的圆的方程；

（3）设直线与圆C交于A，B两点，是否存在实数a，使得直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，说明理由．

【题目】近年来，共享单车已经悄然进入了广大市民的日常生活，并慢慢改变了人们的出行方式.为了更好地服务民众，某共享单车公司在其官方中设置了用户评价反馈系统，以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出条较为详细的评价信息进行统计，车辆状况的优惠活动评价的列联表如下：

（1）能否在犯错误的概率不超过的前提下认为优惠活动好评与车辆状况好评之间有关系？

（2）为了回馈用户，公司通过向用户随机派送骑行券.用户可以将骑行券用于骑行付费，也可以通过转赠给友.某用户共获得了张骑行券，其中只有张是一元券.现该用户从这张骑行券中随机选取张转赠给好友，求选取的张中至少有张是一元券的概率.

参考数据：

参考公式：，其中.