【题目】已知在正整数n的各位数字中，共含有个1，个2，，个n．证明：并确定使等号成立的条件．

【题目】在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，已知曲线的极坐标方程为，过点的直线的参数方程为（为参数），直线与曲线相交于，两点.

（1）写出曲线的直角坐标方程和直线的普通方程；

（2）若，求的值.

【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5]分成9组，制成了如图所示的频率分布直方图.

（Ⅰ）求直方图中a的值；

（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；

（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.

【题目】已知函数.

（1）若是的导函数，讨论的单调性；

（2）若（是自然对数的底数），求证：.

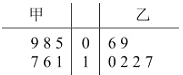
（1）求甲命中个数的中位数和乙命中个数的众数；

（2）通过计算，比较甲乙两人的罚球水平.

【题目】如图，在四棱锥中，平面，， ，，，，为侧棱上一点.

（1）若，求证：平面；

（2）求证：平面平面；

（3）在侧棱上是否存在点，使得平面？ 若存在，求出线段的长；若不存在，请说明理由．

【题目】如图，在四棱锥中，底面是平行四边形，且，，平面平面.

（1）求证：；

（2）若底面是边长为2的菱形，四棱锥的体积为，求点到平面的距离.

(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程；

(2)试根据(1)求出的线性回归方程,预测燃放烟花爆竹的天数为9的雾霾天数.

(相关公式：)

【题目】假设要考察某公司生产的克袋装牛奶的质量是否达标，现从袋牛奶中抽取袋牛奶进行检验，利用随机数表抽样时，先将袋牛奶按、、、进行编号，如果从随机数表第行第列开始向右读，请你依次写出最先检测的袋牛奶的编号_____________，_____________，_____________，_____________，_____________.（下面摘取了随机数表第行至第行）

8842 1753 3157 2455 0688 7704 7476 7217 6335 0258 3921 2067 64

6301 6378 5916 9556 6719 9810 5071 7512 8673 5807 4439 5238 79

3321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 54

【题目】已知函数 ，x R其中a>0.

（Ⅰ）求函数f(x)的单调区间；

（Ⅱ）若函数f(x)在区间(-3,0)内恰有两个零点，求a的取值范围；

（Ⅲ）当a=1时，设函数f(x)在区间[t,t+3]上的最大值为M(t)，最小值为m(t),记 ,求函数g(t)在区间[-4,-1]上的最小值.