【题目】如图,在四棱锥中,平面 平面,BC//平面PAD, ,.

求证:(1) 平面；

(2)平面平面.

【题目】（1）已知，求的定义域并判断奇偶性.

（2）已知奇函数定义域为R，时，，求解析式.

（3）已知函数，求单调增区间和减区间.

【题目】已知函数是定义在实数集R上的奇函数，且在区间上是单调递增，若，则的取值范围为_______．

【题目】经统计分析，我市城区某拥挤路段的车流速度v（单位：千米/小时）是车流密度x（单位：辆/千米）的函数.当该路段的车流密度达到180辆/千米时，造成堵塞，此时车流速度为0千米/小时；当车流密度不超过20辆/千米时，车流速度为40千米/小时；当时，车流速度v是车流密度x的一次函数.

（1）当时，求函数的表达式；

（2）当车流密度x为多大时，该拥挤路段车流量（单位时间内通过该路段某观测点的车辆数，单位：辆/小时）可以达到最大，并求出最大值（精确到1辆/小时）.

【题目】已知函数，关于x的方程，下列四个结论中正确的有（ ）

①存在实数k，使得方程恰有2个不同的实根；

②存在实数k，使得方程恰有4个不同的实根；

③存在实数k，使得方程恰有5个不同的实根；

④存在实数k，使得方程恰有8个不同的实根.

A.1个B.2个C.3个D.4个

【题目】已知二次函数满足:，的最小值为1，且在轴上的截距为4.

(1)求此二次函数的解析式；

(2)若存在区间，使得函数的定义域和值域都是区间，则称区间为函数的“不变区间”.试求函数的不变区间；

(3)若对于任意的，总存在，使得，求的取值范围.

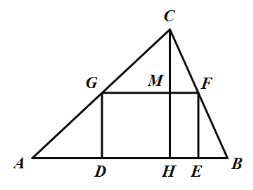
【题目】某市有一面积为12000平方米的三角形地块，其中边长为200米，现计划建一个如图所示的长方形停车场，停车场的四个顶点都在的三条边上，其余的地面全部绿化.若建停车场的费用为180元/平方米，绿化的费用为60元/平方米，设米，建设工程的总费用为元.

（1）求关于的函数表达式：

（2）求停车场面积最大时的值，并求此时的工程总费用.

【题目】从全校参加科技知识竞赛初赛的学生试卷中，抽取一个样本，考察竞赛的成绩分布.将样本分成5组，绘成频率分布直方图（如图），图中从左到右各小组的小长方形的高之比是，最后一组的频数是6.请结合频率分布直方图提供的信息，解答下列问题：

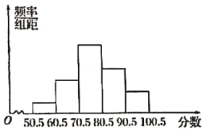
（1）样本的容量是多少?

（2）求样本中成绩在分的学生人数；

（3）从样本中成绩在90.5分以上的同学中随机地抽取2人参加决赛，求最高分甲被抽到的概率.

【题目】已知函数，其中为常数，为自然对数的底数．

（1）当时，求的最大值；

（2）若在区间上的最大值为，求的值．

【题目】已知椭圆 的离心率为，过椭圆的焦点且与长轴垂直的弦长为1．

（1）求椭圆C的方程；

（2）设点M为椭圆上第一象限内一动点，A，B分别为椭圆的左顶点和下顶点，直线MB与x轴交于点C，直线MA与y轴交于点D，求证：四边形ABCD的面积为定值．