
科目: 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和
项和![]() ,已知
,已知![]() ,
,![]() .
.
(1)求证:数列![]() 为等差数列,并求出其通项公式;
为等差数列,并求出其通项公式;
(2)设![]() ,又
,又![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() 为正整数且
为正整数且![]() ,数列
,数列![]() 共有
共有![]() 项,设
项,设![]() ,又
,又![]() ,求
,求![]() 的所有可能取值.
的所有可能取值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业生产某种商品![]() 吨,此时所需生产费用为(
吨,此时所需生产费用为(![]() )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为![]() 万元,这里
万元,这里![]() (
(![]() 为常数,
为常数,![]() )
)
(1)为了使这种商品的生产费用平均每吨最低,那么这种商品的产量应为多少吨?
(2)如果生产出来的商品能全部卖完,当产量是120吨时企业利润最大,此时出售价格是每吨160万元,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,半径为
,半径为![]() .
.
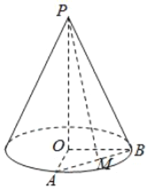
(1)设圆锥的母线长为![]() ,求圆锥的体积;
,求圆锥的体积;
(2)设![]() ,
,![]() 、
、![]() 是底面半径,且
是底面半径,且![]() ,
,![]() 为线段
为线段![]() 的中点,如图.求异面直线
的中点,如图.求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上恰有一个实数解,求
上恰有一个实数解,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若存在
,若存在![]() 使得函数
使得函数![]() 在区间
在区间![]() 上的最大值和最小值的差不超过1,求
上的最大值和最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利,根据大数据统计,某条地铁线路运行时,发车时间间隔![]() (单位:分钟)满足:
(单位:分钟)满足: ![]() ,平均每班地铁的载客人数
,平均每班地铁的载客人数![]() (单位:人)与发车时间间隔
(单位:人)与发车时间间隔![]() 近似地满足函数关系:
近似地满足函数关系: ,
,
(1)若平均每班地铁的载客人数不超过1560人,试求发车时间间隔![]() 的取值范围;
的取值范围;
(2)若平均每班地铁每分钟的净收益为![]() (单位:元),则当发车时间间隔
(单位:元),则当发车时间间隔![]() 为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足:①对一切
满足:①对一切![]() 恒有
恒有![]() ;②对一切
;②对一切![]() 恒有
恒有![]() ;③当
;③当![]() 时,
时,![]() ,且
,且![]() ;④若对一切
;④若对一切![]() (其中
(其中![]() ),不等式
),不等式![]() 恒成立.
恒成立.
(1)求![]() 的值;
的值;
(2)证明:函数![]() 是
是![]() 上的递增函数;
上的递增函数;
(3)求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,梯形ABCD所在的平面与等腰梯形ABEF所在的平面互相垂直,AB∥CD∥EF,AB⊥AD,CD=DA=AF=FE=2,AB=4.
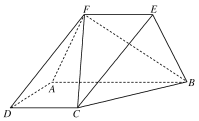
(1)求证:DF∥平面BCE;
(2)求二面角C—BF—A的正弦值;
(3)线段CE上是否存在点G,使得AG⊥平面BCF?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com