
科目: 来源: 题型:
【题目】榆林市政府坚持保护环境和节约资源,坚持推进生态文明建设。若市财政局下拨专款100百万元,分别用于植绿护绿和处理污染两个生态维护项目,植绿护绿项目五年内带来的生态收益可表示为投放资金![]() (单位:百万元)的函数
(单位:百万元)的函数![]() (单位:百万元):
(单位:百万元):![]() ,处理污染项目五年内带来的生态收益可表示为投放资金
,处理污染项目五年内带来的生态收益可表示为投放资金![]() 单位:(单位:百万元)的函数
单位:(单位:百万元)的函数![]() (单位:百万元):
(单位:百万元):![]() 。
。
(1)设分配给植绿护绿项目的资金为![]() (百万元),则两个生态项目五年内带来的收益总和为y,写出y关于
(百万元),则两个生态项目五年内带来的收益总和为y,写出y关于![]() 的函数解析式和定义域;
的函数解析式和定义域;
(2)试求出y的最大值,并求出此时对两个生态项目的投资分别为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】设y=f(x)在(-∞,1]上有定义,对于给定的实数K,定义fK(x)=![]() ,给出函数f(x)=2x+1-4x,若对于任意x∈(-∞,1],恒有fK(x)=f(x),则( )
,给出函数f(x)=2x+1-4x,若对于任意x∈(-∞,1],恒有fK(x)=f(x),则( )
A.K的最大值为0
B.K的最小值为0
C.K的最大值为1
D.K的最小值为1
查看答案和解析>>
科目: 来源: 题型:
【题目】我国南宋数学家杨辉所著的![]() 详解九章算术
详解九章算术![]() 一书中,用图
一书中,用图![]() 的数表列出了一些正整数在三角形中的一种几何排列,俗称“杨辉三角形”,该数表的规律是每行首尾数字均为1,从第三行开始,其余的数字是它“上方”左右两个数字之和
的数表列出了一些正整数在三角形中的一种几何排列,俗称“杨辉三角形”,该数表的规律是每行首尾数字均为1,从第三行开始,其余的数字是它“上方”左右两个数字之和![]() 现将杨辉三角形中的奇数换成1,偶数换成0,得到图
现将杨辉三角形中的奇数换成1,偶数换成0,得到图![]() 所示的由数字0和1组成的三角形数表,由上往下数,记第n行各数字的和为
所示的由数字0和1组成的三角形数表,由上往下数,记第n行各数字的和为![]() ,如
,如![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]()
![]()

A. 2 B. 4 C. 8 D. 16
查看答案和解析>>
科目: 来源: 题型:
【题目】出租车几何学是由十九世纪的赫尔曼·闵可夫斯基所创立的。在出租车几何学中,点还是形如![]() 的有序实数对,直线还是满足
的有序实数对,直线还是满足![]() 的所有
的所有![]() 组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样,直角坐标系内任意两点![]() 定义它们之间的一种“距离”:
定义它们之间的一种“距离”:![]() ,请解决以下问题:
,请解决以下问题:
(1)求线段![]() 上一点
上一点![]() 到点
到点![]() 的“距离”;
的“距离”;
(2)定义:“圆”是所有到定点“距离”为定值的点组成的图形,求“圆”上的所有点到点![]() 的“距离”均为
的“距离”均为![]() 的“圆”方程,并求该“圆”围成的图形的面积;
的“圆”方程,并求该“圆”围成的图形的面积;
(3)若点![]() 到点
到点![]() 的“距离”和点
的“距离”和点![]() 到点
到点![]() 的“距离”相等,其中实数
的“距离”相等,其中实数![]() 满足
满足![]() ,求所有满足条件的点
,求所有满足条件的点![]() 的轨迹的长之和.
的轨迹的长之和.
查看答案和解析>>
科目: 来源: 题型:
【题目】给定平面上的点集![]() ,
,![]() 中任三点均不共线。将
中任三点均不共线。将![]() 中所有的点任意分成83组,使得每组至少有3个点,且每点恰好属于一组,然后将在同一组的任两点用一条线段相连,不在同一组的两点不连线段,这样得到一个图案
中所有的点任意分成83组,使得每组至少有3个点,且每点恰好属于一组,然后将在同一组的任两点用一条线段相连,不在同一组的两点不连线段,这样得到一个图案![]() 。不同的分组方式得到不同的图案。将图案
。不同的分组方式得到不同的图案。将图案![]() 中所含的以
中所含的以![]() 中的点为顶点的三角形的个数记为
中的点为顶点的三角形的个数记为![]() 。
。
(1)求![]() 的最小值
的最小值![]() ;
;
(2)设![]() 是使
是使![]() 的一个图案,若将
的一个图案,若将![]() 中的线段(指以
中的线段(指以![]() 的点为端点的线段)用4种颜色染色,每条线段恰好染一种颜色。证明存在一个染色方案,使
的点为端点的线段)用4种颜色染色,每条线段恰好染一种颜色。证明存在一个染色方案,使![]() 染色后不含以
染色后不含以![]() 的点为顶点的三边颜色相同的三角形。
的点为顶点的三边颜色相同的三角形。
查看答案和解析>>
科目: 来源: 题型:
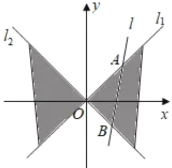
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与直线
与直线![]() 之间的阴影部分记为
之间的阴影部分记为![]() ,区域
,区域![]() 中动点
中动点![]() 到
到![]() 的距离之积为1.
的距离之积为1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)对于区域![]() 中动点
中动点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)动直线![]() 穿过区域
穿过区域![]() ,分别交直线
,分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 有且只有一个公共点,求证:
有且只有一个公共点,求证:![]() 的面积值为定值.
的面积值为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com