（1）若曲线y=f(x)在点(1，f（1）)处的切线方程为y=x，求a、b的值；

（2）若f(x)≤x2+x恒成立，求ab的最大值.

【题目】已知函数f（x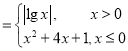），g（x）=f（x）-a，

（1）讨论函数g（x）的零点个数，并写出相应的实数a的取值范围；

（2）当函数g（x）有四个零点分别为x1，x2，x3，x4时，求x1+x2+x3+x4的取值范围.

【题目】在△ABC中，a，b，c分别为内角A，B，C的对边，且asin B＝－bsin.

(1)求A；

(2)若△ABC的面积S＝c2，求sin C的值．

【题目】古希腊数学家阿波罗尼奧斯（约公元前262～公元前190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，他证明过这样一个命题：平面内与两定点距离的比为常数k（k＞0，k≠1）的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆．在平面直角坐标系中，设A（﹣3，0），B（3，0），动点M满足＝2，则动点M的轨迹方程为（）

A. （x﹣5）2+y2＝16B. x2+（y﹣5）2＝9

C. （x+5）2+y2＝16D. x2+（y+5）2＝9

【题目】已知变量、之间的线性回归方程为，且变量、之间的一-组相关数据如下表所示，则下列说法错误的是（ ）

A.可以预测，当时，B.

C.变量之间呈负相关关系D.该回归直线必过点

（1）求通项公式an；

（2）设，为数列｛bn｝的前n项和，求正整数k，使得对任意的n∈Z+，均有T4≥Tn；

（3）设，Rn为数列{cn}的前n项和，若对任意的n∈Z+，均有Rn<λ，求λ的最小值.

【题目】已知函数（a为实常数）.

（1）若，作函数的图象并写出单调减区间；

（2）当时，设在区间上的最小值为，求的表达式；

（3）当时对于函数和函数，若对任意的，总存在使成立，求实数m的值.

（Ⅰ）分别求A∩B，（RB）∪A；

（Ⅱ）已知集合C＝{x|1＜x＜a}，若CA，求实数a的取值集合．

①“若，则”的逆否命题为真命题

②“”是“函数在区间上为增函数”的充分不必要条件

③若为假命题，则，均为假命题

④对于命题：，，则为：，

其中真命题的个数是（ ）

A.1个B.2个C.3个D.4个