
科目: 来源: 题型:
【题目】在直角坐标系xOy中,已知曲线C1:![]() (α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρcos
(α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρcos ![]() =-
=-![]() ,曲线C3:ρ=2sin θ.
,曲线C3:ρ=2sin θ.
(1)求曲线C1与C2的交点M的直角坐标;
(2)设点A,B分别为曲线C2,C3上的动点,求|AB|的最小值.
查看答案和解析>>
科目: 来源: 题型:
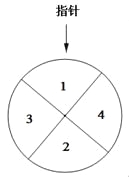
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() :
:![]() ,过抛物线焦点
,过抛物线焦点![]() 且与
且与![]() 轴垂直的直线与抛物线相交于
轴垂直的直线与抛物线相交于![]() 、
、![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 过焦点
过焦点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 、
、![]() ,切线
,切线![]() 与
与![]() 相交于点
相交于点![]() ,求:
,求:![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
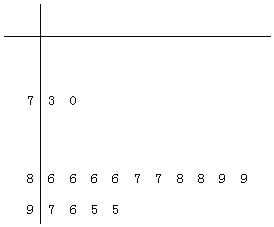
【题目】陕西理工大学开展大学生社会实践活动,用“10分制”随机调查汉台区某社区居民的幸福指数,现从调查人群中随机抽取16人,如图所示的茎叶图记录了他们的幸福指数的得分![]() 以小数点的前一位数字为茎,小数点后的一位数字为叶
以小数点的前一位数字为茎,小数点后的一位数字为叶![]() :
:
![]() 写出这组数据的众数和中位数;
写出这组数据的众数和中位数;
![]() 若幸福指数不低于9分,则称该人的幸福指数为“极幸福”;若幸福指数不高于8分,则称该人的幸福指数为“不够幸福”
若幸福指数不低于9分,则称该人的幸福指数为“极幸福”;若幸福指数不高于8分,则称该人的幸福指数为“不够幸福”![]() 现从这16人中幸福指数为“极幸福”和“不够幸福”的人中任意选取2人,求选出的两人的幸福指数均为“极幸福”的概率.
现从这16人中幸福指数为“极幸福”和“不够幸福”的人中任意选取2人,求选出的两人的幸福指数均为“极幸福”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.

(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 1 | 3 | 4 | 7 |
表中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入上表的空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
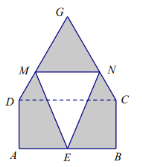
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部![]() 是矩形,其中
是矩形,其中![]() 米,
米,![]() 米;上部
米;上部![]() 是等边三角形,固定点
是等边三角形,固定点![]() 为
为![]() 的中点.
的中点.![]() 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),
是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),![]() 是可以沿设施边框上下滑动且始终保持和
是可以沿设施边框上下滑动且始终保持和![]() 平行的伸缩横杆.
平行的伸缩横杆.
(1)设![]() 与
与![]() 之间的距离为
之间的距离为![]() 米,试将
米,试将![]() 的面积
的面积![]() (平方米)表示成关于
(平方米)表示成关于![]() 的函数;
的函数;
(2)求![]() 的面积
的面积![]() (平方米)的最大值.
(平方米)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com