
科目: 来源: 题型:
【题目】(13分)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC中点,PO⊥平面ABCD,PO=2,M为PD中点.

(Ⅰ)证明:PB∥平面ACM;
(Ⅱ)证明:AD⊥平面PAC;
(Ⅲ)求直线AM与平面ABCD所成角的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为响应“生产发展、生活富裕、乡风文明、村容整洁、管理民主”的社会主义新农村建设,某自然村将村边一块废弃的扇形荒地(如图)租给蜂农养蜂、产蜜与售蜜.已知扇形AOB中,![]() ,
,![]() 百米),荒地内规划修建两条直路AB,OC,其中点C在弧AB上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设
百米),荒地内规划修建两条直路AB,OC,其中点C在弧AB上(C与A,B不重合),在小路AB与OC的交点D处设立售蜜点,图中阴影部分为蜂巢区,空白部分为蜂源植物生长区.设![]() ,蜂巢区的面积为S(平方百米).
,蜂巢区的面积为S(平方百米).

(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,蜂巢区的面积S最小,并求此时S的最小值.
为何值时,蜂巢区的面积S最小,并求此时S的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为正方形,平面
中,底面ABCD为正方形,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,E,F分别为AD,PB的中点.
,E,F分别为AD,PB的中点.
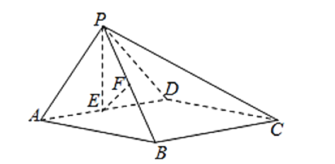
(1)求证:![]() 平面ABCD;
平面ABCD;
(2)求证:![]() 平面PCD;
平面PCD;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某产品的三个质量指标分别为x, y, z, 用综合指标S =" x" + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 现从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标(x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标(x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(Ⅰ) 利用上表提供的样本数据估计该批产品的一等品率;
(Ⅱ) 在该样品的一等品中, 随机抽取两件产品,
(1) 用产品编号列出所有可能的结果;
(2) 设事件B为 “在取出的2件产品中, 每件产品的综合指标S都等于4”, 求事件B发生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国有多个地方盛产板栗,但板栗的销售受季节的影响,储存时间不能太长.某校数学兴趣小组对近几年某食品销售公司的板栗销售量y(吨)和板栗的销售单价x(元/千克)之间的关系进行了调查,得到下表数据:
销售单价x(元/千克) | 11 | 10.5 | 10 | 9.5 | 9 | 8 |
销售量y(吨) | 5 | 6 | 8 | 10 | 11 | 14.1 |
(1)根据前5组数据,求出y关于x的线性回归方程;
(2)若线性回归方程得到的估计数据与剩下的检验数据的误差不超过0.5,则认为线性回归方程是理想的,试问(1)中得到的线性回归方程是否理想?
(附:线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】对于给定数列![]() ,若数列
,若数列![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“相伴数列”.
的“相伴数列”.
(1)若![]() ,且数列
,且数列![]() 是数列
是数列![]() 的“相伴数列”,试写出
的“相伴数列”,试写出![]() 的一个通项公式,并说明理由;
的一个通项公式,并说明理由;
(2)设![]() ,证明:不存在等差数列
,证明:不存在等差数列![]() ,使得数列
,使得数列![]() 是数列
是数列![]() 的“相伴数列”;
的“相伴数列”;
(3)设![]() ,
,![]() (其中
(其中![]() ),若
),若![]() 是数列
是数列![]() 的“相伴数列”,试分析实数b、q的取值应满足的条件.
的“相伴数列”,试分析实数b、q的取值应满足的条件.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线T上的任意一点到两定点![]() 的距离之和为
的距离之和为![]() ,直线l交曲线T于A、B两点,
,直线l交曲线T于A、B两点,![]() 为坐标原点.
为坐标原点.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 不过点
不过点![]() 且不平行于坐标轴,记线段AB的中点为M,求证:直线
且不平行于坐标轴,记线段AB的中点为M,求证:直线![]() 的斜率与l的斜率的乘积为定值;
的斜率与l的斜率的乘积为定值;
(3)若OA![]() OB,求△
OB,求△![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com