（1）试估计使用A款订餐软件的50个商家的“平均送达时间”的众数及平均数（同一组中的数据用该组区间的中点值作代表）.

（2）根据以上抽样调查数据，将频率视为概率，回答下列问题：

①能否认为使用B款订餐软件“平均送达时间”不超过40分的商家达到75%？

②如果你要从A和B两款订餐软件中选择一款订餐，你会选择哪款？说明理由.

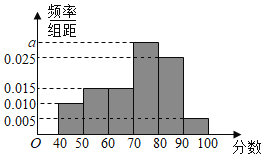
【题目】某校从高二年级学生中随机抽取60名学生，将期中考试的政治成绩（均为整数）分成六段：后得到如下频率分布直方图．

（1）根据频率分布直方图，分别求，众数，中位数。

（2）估计该校高二年级学生期中考试政治成绩的平均分。

（3）用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本，则在分数段抽取的人数是多少？

（1）求数列{an}的通项公式；

（2）令bn，设数列{bn}的前项和为Tn，若Tn，求n的最小值.

【题目】关于统计数据的分析，有以下几个结论：①将一组数据中的每个数据都减去同一个数后，方差没有变化；②绘制频率分布直方图时，各小长方形的面积等于相应各组的组距；③一组数据的方差一定是正数；④如图是随机抽取的200辆汽车通过某一段公路时的时速分布直方图，根据这个直方图，可以得到时速在的汽车大约是60辆.则这4个结论中错误的个数是（ ）

A.1B.2C.3D.4

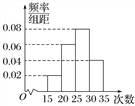
A. 该校九年级学生1分钟仰卧起坐的次数的中位数为26.25

B. 该校九年级学生1分钟仰卧起坐的次数的众数为27.5

C. 该校九年级学生1分钟仰卧起坐的次数超过30次的约有320人

D. 该校九年级学生1分钟仰卧起坐的次数少于20次的约有32人

【题目】已知函数.

当时，恒成立，求的值；

若恒成立，求的最小值.

郊区：19 25 28 32 34

城区：18 19 21 22 22 23 23 23 24 25 26 27 28 28 28 29 29 31 35 42

（1）在郊区的这5户居民中随机抽取2户，求其年人均用水量都不超过30吨的概率；

（2）设该城市郊区和城区的居民户数比为1：5，现将年人均用水量不超过30吨的用户定义为第一阶梯用户，并保证这一阶梯的居民用户用水价格保持不变，试根据样本总体的思想，分析此方案是否符合国家“保基本”政策.

【题目】已知函数.

（1）求函数的极值；

（2）设函数，若存在，使，证明：.

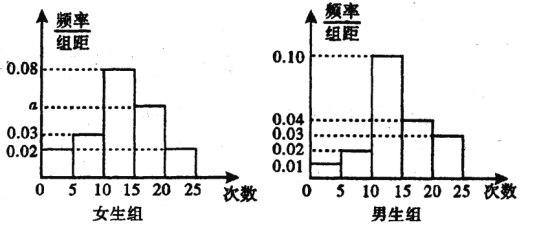
【题目】某中学为了了解全校学生的上网情况，在全校采用随机抽样的方法抽取了 40 名学生（其中男女生人数恰好各占一半）进行问卷调查，并进行了统计，按男女分为两组，再将每组学生的月上网次数分为5组：，，，，，得到如图所示的频率分布直方图：

（1）求的值；

（2）求抽取的40名学生中月上网次数不少于15次的人数；

（3）再从月上网次数不少于20 次的学生中随机抽取2人，求至少抽到1名女生的概率.