【题目】在直角坐标系中，以坐标原点为极点，以轴正半轴为极轴建立极坐标系，已知曲线的极坐标方程为.

（1）求曲线的直角坐标方程；

（2）若两条互相垂直的直线都经过原点（两条直线与坐标轴都不重合）且与曲线分别交于点（异于原点），且，求这两条直线的直角坐标方程.

（1）求C的直角坐标方程；

（2）若l与C交于A，B两点，求的最大值.

【题目】随机抽取某校高一100名学生的期末考试英语成绩（他们的英语成绩都在80分140分之间），将他们的英语成绩（单位：分）分成：，，，，六组，得到如图所示的部分频率分布直方图，已知成绩处于内与内的频数之和等于成绩处于内的频数，根据图中的信息，回答下列问题：

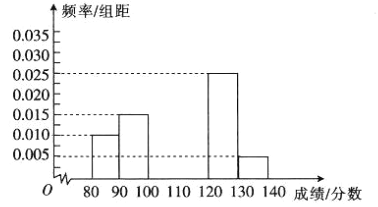
（1）求频率分布直方图中未画出的小矩形的面积之和；

（2）求成绩处于内与内的频率之差；

（3）用分层抽样的方法从成绩不低于120分的学生中选取一个容量为6的样本，将该样本看成一个总体，从中任选2人，求这2人中恰有一人成绩低于130分的概率.

①甲地5个数据的中位数为24，众数为22；

②乙地5个数据的中位数为27，总体均值为24；

③丙地5个数据中有一个数据是32，总体均值为26，总体方差为10.8.

则肯定进入夏季的地区有_____．

【题目】《九章算术》是中国古代的数学专著，其中的“更相减损术”可以用来求两个数的最大公约数，原文是：可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也，以等数约之. 翻译为现代的语言如下：如果需要对分数进行约分，那么可以折半的话，就折半（也就是用2来约分）.如果不可以折半的话，那么就比较分母和分子的大小，用大数减去小数，互相减来减去，一直到减数与差相等为止，用这个相等的数字来约分，现给出“更相减损术”的程序框图如图所示，如果输入的，，则输出的（ ）

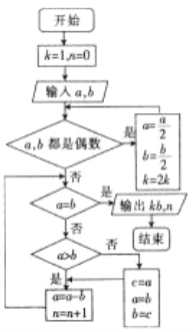
A. 6 B. 5 C. 4 D. 3

（1）求角A的大小；

（2）若AB=3，AC边上的中线SD的长为，求△ABC的面积．

【题目】我国上是世界严重缺水的国家，城市缺水问题较为突出，某市政府为了鼓励居民节约用水，计划在本市试行居民生活用水定额管理，即确定一个合理的居民月用水量标准（吨），用水量不超过的部分按平价收费，超过的部分按议价收费，为了了解全市民月用水量的分布情况，通过抽样，获得了100位居民某年的月用水量（单位：吨），将数据按照， ，…， 分成9组，制成了如图所示的频率分布直方图.

（Ⅰ）求直方图中 的值；

（Ⅱ）已知该市有80万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；

（Ⅲ）若该市政府希望使的居民每月的用水量不超过标准（吨），估计的值，并说明理由；

【题目】如图，在四棱锥中，底面是矩形，为的中点，底面，.

（1）求证：平面；

（2）求钝二面角的余弦值.

【题目】在直角坐标系中，以坐标原点为极点，以轴正半轴为极轴建立极坐标系，已知曲线的极坐标方程为.

（1）求曲线的直角坐标方程；

（2）若两条互相垂直的直线都经过原点（两条直线与坐标轴都不重合）且与曲线分别交于点（异于原点），且，求这两条直线的直角坐标方程.

【题目】某工厂对一批新产品的长度(单位：)进行检测，如下图是检测结果的频率分布直方图，据此估计这批产品的中位数与平均数分别为( )

A.20，22.5B.22.5，25C.22.5，22.75D.22.75，22.75