
科目: 来源: 题型:
【题目】如图,将边长为2的正方形ABCD沿PD、PC翻折至A、B两点重合,其中P是AB中点,在折成的三棱锥A(B)-PDC中,点Q在平面PDC内运动,且直线AQ与棱AP所成角为60,则点Q运动的轨迹是
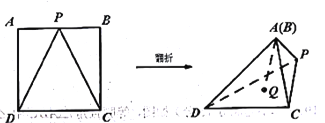
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线C1的参数方程为![]() (t为参数),以该直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系下,圆C2的方程为ρ=﹣2cosθ+2
(t为参数),以该直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系下,圆C2的方程为ρ=﹣2cosθ+2![]() sinθ.
sinθ.
(Ⅰ)求直线C1的普通方程和圆C2的圆心的极坐标;
(Ⅱ)设直线C1和圆C2的交点为A,B,求弦AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得.1 000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C).
(2)1张奖券的中奖概率.
(3)1张奖券不中特等奖,且不中一等奖的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]()
![]() .
.
(1)判断直线![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)若![]() 是曲线
是曲线![]() 上的动点,求
上的动点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名中学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段: ![]() ,
, ![]() ,…,
,…, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(1)求图中实数![]() 的值;
的值;
(2)若该校高一年级共有640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
推出的多款健康运动软件中的一款,某学校140名老师均在微信好友群中参与了“微信运动”,对运动10000步或以上的老师授予“运动达人”称号,低于10000步称为“参与者”,为了解老师们运动情况,选取了老师们在4月28日的运动数据进行分析,统计结果如下:
运动达人 | 参与者 | 合计 | |
男教师 | 60 | 20 | 80 |
女教师 | 40 | 20 | 60 |
合计 | 100 | 40 | 140 |
(Ⅰ)根据上表说明,能否在犯错误概率不超过0.05的前提下认为获得“运动达人”称号与性别有关?
(Ⅱ)从具有“运动达人”称号的教师中,采用按性别分层抽样的方法选取10人参加全国第四届“万步有约”全国健走激励大赛某赛区的活动,若从选取的10人中随机抽取3人作为代表参加开幕式,设抽取的3人中女教师人数为![]() ,写出
,写出![]() 的分布列并求出数学期望
的分布列并求出数学期望![]() .
.
参考公式: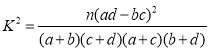 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下面类比推理:
①“若2a<2b,则a<b”类比推出“若a2<b2,则a<b”;
②“(a+b)c=ac+bc(c≠0)”类比推出“![]() (c≠0)”;
(c≠0)”;
③“a,b∈R,若a-b=0,则a=b”类比推出“a,b∈C,若a-b=0,则a=b”;
④“a,b∈R,若a-b>0,则a>b”类比推出“a,b∈C,若a-b>0,则a>b(C为复数集)”.
其中结论正确的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com