
科目: 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
![]()
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前,100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
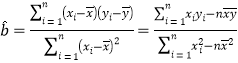 ,参考数值:
,参考数值:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】渔民出海打鱼,为了保证获得的鱼新鲜,鱼被打上岸后,要在最短的时间内将其分拣、冷藏,若不及时处理,打上来的鱼很快地失去新鲜度(以鱼肉内的三甲胺量的多少来确定鱼的新鲜度.三甲胺是一种挥发性碱性氨,是氨的衍生物,它是由细菌分解产生的.三甲胺量积聚就表明鱼的新鲜度下降,鱼体开始变质进而腐败).已知某种鱼失去的新鲜度![]() 与其出海后时间
与其出海后时间![]() (分)满足的函数关系式为
(分)满足的函数关系式为![]() .若出海后10分钟,这种鱼失去的新鲜度为10%,出海后20分钟,这种鱼失去的新鲜度为20%,那么若不及时处理,打上来的这种鱼在多长时间后开始失去全部新鲜度(已知
.若出海后10分钟,这种鱼失去的新鲜度为10%,出海后20分钟,这种鱼失去的新鲜度为20%,那么若不及时处理,打上来的这种鱼在多长时间后开始失去全部新鲜度(已知![]() ,结果取整数)( )
,结果取整数)( )
A.33分钟B.40分钟C.43分钟D.50分钟
查看答案和解析>>
科目: 来源: 题型:
【题目】给定一个由![]() 个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
个小正方形拼成的棋盘形方格,这些小正方形的颜色黑白相间(如图).
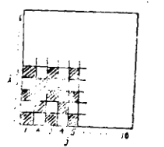
现定义一种运算A:把位于第i行的所有小正方形和位于第j列的所有小正方形都换成相反的颜色,即黑色的小正方形换成白色的,白色的小正方形换成黑色的,这里![]() .我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
.我们把A称为在位于第i行第j列上的小正方形上的一次运算.试问:能否经过若干次上述运算把棋盘上的所有小正方形全部换成同一种颜色?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知矩形ABCD中,![]() ,
,![]() ,M是以CD为直径的半圆周上的任意一点(与C,D均不重合),且平面
,M是以CD为直径的半圆周上的任意一点(与C,D均不重合),且平面![]() 平面ABCD.
平面ABCD.
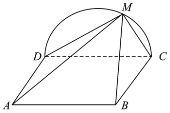
(1)求证:平面![]() 平面BCM;
平面BCM;
(2)当四棱锥![]() 的体积最大时,求AM与CD所成的角.
的体积最大时,求AM与CD所成的角.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四个命题
①若三个平面两两相交,则它们的交线只能平行或重合;
②若a、b是异面直线,则过不在a、b上的任一点一定可以作一条直线和a、b都相交;
③正三棱锥![]() 的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为
的底面边长为a,侧棱长为b,若过SA、SB的中点作平行于侧棱SC的截面,则截面面积为![]() ;
;
④过球面上任意给定两点的平面与球面相截时其截面面积最大,则这样的平面只有一个.
其中( ).
A. 只有①,②成立.
B. 只有③成立.
C. 只有④ 成立.
D. ①、②、③、④都不成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(2)设函数![]() ,当
,当![]() 时,
时,![]() 有且只有一个实数根,求
有且只有一个实数根,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,设P、M、N分别是正方体的棱![]() ,AD,AB上非顶点的任意点.
,AD,AB上非顶点的任意点.
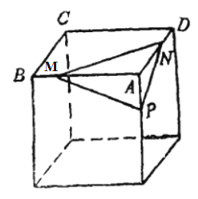
①![]() 的外心必在
的外心必在![]() 的某一边上;
的某一边上;
②![]() 的外心必在
的外心必在![]() 的内部;
的内部;
③![]() 的垂心必是点A在平面PMN上的射影;
的垂心必是点A在平面PMN上的射影;
④若线段AP、AM、AN的长分别为a、b、c,则![]() .其中( ).
.其中( ).
A. 只有①、④正确.
B. 只有③、④正确.
C. 只有②、③、④正确.
D. 只有②、③正确.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水.已知该厂生活用水为每小时10吨,生产用水量![]() (吨)与时间
(吨)与时间![]() (单位:小时,且规定早上6时
(单位:小时,且规定早上6时![]() )的函数关系式为:
)的函数关系式为:![]() ,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
,水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管.
(1)若进水量选择为![]() 级,水塔中剩余水量为
级,水塔中剩余水量为![]() 吨,试写出
吨,试写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)如何选择进水量,既能始终保证该厂的用水(水塔中水不空)又不会使水溢出?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com