
科目: 来源: 题型:
【题目】某种工业机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:
方案一:交纳延保金700元,在延保的两年内可免费维修2次,超过2次每次收取维修费200元;
方案二:交纳延保金1000元,在延保的两年内可免费维修4次,超过4次每次收取维修费100元.
某工厂准备一次性购买2台这种机器.现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 20 | 10 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率.记X表示这2台机器超过质保期后延保的两年内共需维修的次数.
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,工厂选择哪种延保方案更合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 分别为棱
分别为棱![]() 上的动点(
上的动点(![]() 与所在棱的端点不重合),且满足
与所在棱的端点不重合),且满足![]() .
.
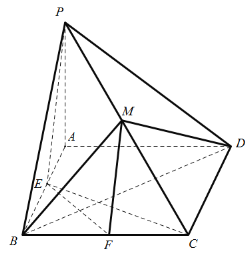
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】数列![]() ,
,![]() 满足下列条件:①
满足下列条件:①![]() ,
,![]() ;②当
;②当![]() 时,
时,![]() 满足:
满足:![]() 时,
时,![]() ,
,![]() ;
;![]() 时,
时,![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 和
和![]() 的值,并猜想数列
的值,并猜想数列![]() 可能的通项公式(不需证明);
可能的通项公式(不需证明);
(2)若![]() ,
,![]() ,
,![]() 是满足
是满足![]() 的最大整数,求
的最大整数,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某地区进行疾病普查,为此要检验每一人的血液,如果当地有![]() 人,若逐个检验就需要检验
人,若逐个检验就需要检验![]() 次,为了减少检验的工作量,我们把受检验者分组,假设每组有
次,为了减少检验的工作量,我们把受检验者分组,假设每组有![]() 个人,把这个
个人,把这个![]() 个人的血液混合在一起检验,若检验结果为阴性,这
个人的血液混合在一起检验,若检验结果为阴性,这![]() 个人的血液全为阴性,因而这
个人的血液全为阴性,因而这![]() 个人只要检验一次就够了,如果为阳性,为了明确这个
个人只要检验一次就够了,如果为阳性,为了明确这个![]() 个人中究竟是哪几个人为阳性,就要对这
个人中究竟是哪几个人为阳性,就要对这![]() 个人再逐个进行检验,这时
个人再逐个进行检验,这时![]() 个人的检验次数为
个人的检验次数为![]() 次.假设在接受检验的人群中,每个人的检验结果是阳性还是阴性是独立的,且每个人是阳性结果的概率为
次.假设在接受检验的人群中,每个人的检验结果是阳性还是阴性是独立的,且每个人是阳性结果的概率为![]() .
.
(Ⅰ)为熟悉检验流程,先对3个人进行逐个检验,若![]() ,求3人中恰好有1人检测结果为阳性的概率;
,求3人中恰好有1人检测结果为阳性的概率;
(Ⅱ)设![]() 为
为![]() 个人一组混合检验时每个人的血需要检验的次数.
个人一组混合检验时每个人的血需要检验的次数.
①当![]() ,
,![]() 时,求
时,求![]() 的分布列;
的分布列;
②是运用统计概率的相关知识,求当![]() 和
和![]() 满足什么关系时,用分组的办法能减少检验次数.
满足什么关系时,用分组的办法能减少检验次数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}满足![]() an+1
an+1![]() an=0(n∈N*),且
an=0(n∈N*),且![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求数列{an}的通项公式;
(2)令bn=![]() (n∈N*),求数列{bn}的前n项和为
(n∈N*),求数列{bn}的前n项和为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】杨辉三角是二项式系数在三角形中的一种排列,在欧洲这个表叫做帕斯卡三角形,帕斯卡是在1654年发现这一规律的,我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中出现了如图所示的表,这是我国数学史上的一次伟大成就,如图所示,在“杨辉三角”中去除所有为1的项,依次构成数列,2,3,3,4,6,4,5 ,10 ,10,5,……,则此数列的前119项的和为__________.(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的两个三等分点.若把等腰梯形沿虚线
的两个三等分点.若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() ,如图(2).
,如图(2).
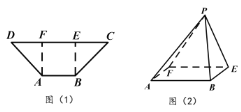
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】经过多年的努力,炎陵黄桃在国内乃至国际上逐渐打开了销路,成为炎陵部分农民脱贫致富的好产品.为了更好地销售,现从某村的黄桃树上随机摘下了100个黄桃进行测重,其质量分布在区间![]() 内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
内(单位:克),统计质量的数据作出其频率分布直方图如图所示:
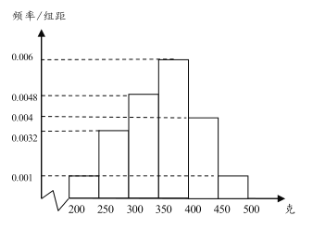
(1)按分层抽样的方法从质量落在![]() ,
,![]() 的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
的黄桃中随机抽取5个,再从这5个黄桃中随机抽2个,求这2个黄桃质量至少有一个不小于400克的概率;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该村的黄桃树上大约还有100000个黄桃待出售,某电商提出两种收购方案:
A.所有黄桃均以20元/千克收购;
B.低于350克的黄桃以5元/个收购,高于或等于350克的以9元/个收购.
请你通过计算为该村选择收益最好的方案.
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com