
科目: 来源: 题型:
【题目】如图是2020年2月1日到2月20日,某地区新型冠状病毒疫情新增数据的走势图.
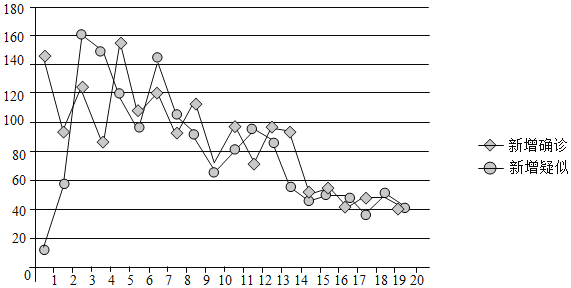
(Ⅰ)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(Ⅱ)从新增确诊的人数超过100的日期中任选两天,用X表示新增确诊的人数超过140的天数,求X的分布列和数学期望;
查看答案和解析>>
科目: 来源: 题型:
【题目】为了调查患胃病是否与生活不规律有关,在患胃病与生活不规律这两个分类变量的计算中,下列说法正确的是( )
A.![]() 越大,“患胃病与生活不规律没有关系”的可信程度越大.
越大,“患胃病与生活不规律没有关系”的可信程度越大.
B.![]() 越大,“患胃病与生活不规律有关系”的可信程度越小.
越大,“患胃病与生活不规律有关系”的可信程度越小.
C.若计算得![]() ,经查临界值表知
,经查临界值表知![]() ,则在
,则在![]() 个生活不规律的人中必有
个生活不规律的人中必有![]() 人患胃病.
人患胃病.
D.从统计量中得知有![]() 的把握认为患胃病与生活不规律有关,是指有
的把握认为患胃病与生活不规律有关,是指有![]() 的可能性使得推断出现错误.
的可能性使得推断出现错误.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() ,
, ![]() 是过点
是过点![]() 且互相垂直的两条直线,其中
且互相垂直的两条直线,其中![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 交椭圆
交椭圆![]() 于另一个点
于另一个点![]() ,求
,求![]() 面积取得最大值时直线
面积取得最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线的顶点在原点,圆![]() 的圆心恰是抛物线的焦点.
的圆心恰是抛物线的焦点.

(1)求抛物线的方程;
(2)一条直线的斜率等于2,且过抛物线焦点,它依次截抛物线和圆于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求
四点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: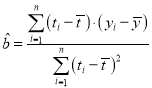 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出表中数据的散点图;
(2)请根据表中提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗多少吨标准煤?
(附: ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com