
科目: 来源: 题型:
【题目】设关于x的方程x2﹣ax﹣1=0和3x2﹣6x+3﹣2a=0的实根分别为x1,x2和x3,x4.若x1<x3<x2<x4,则实数a的取值范围为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:

设农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() =bx+a;
=bx+a;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注:![]() =
= =
= ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,![]() 是等边三角形,D.E分别是BC.AC上两点,且
是等边三角形,D.E分别是BC.AC上两点,且![]() ,
,![]() 与AD交于点H,链接CH.
与AD交于点H,链接CH.
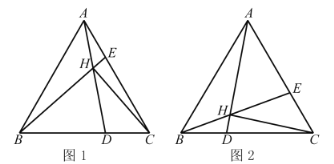
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)如图2,当![]() 时,
时,![]() __________;
__________;![]() __________.
__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校开展主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、待合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.请根据以下信息,解答下列问题:
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 |
| 40% |
合格 | 6 |
|
待合格 | 3 | 6% |
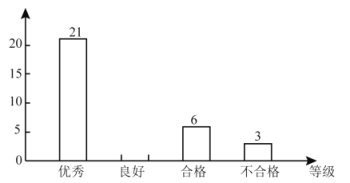
(1)本次调查随机抽取了__________名学生,表中![]() __________,
__________,![]() __________;
__________;
(2)补全条形统计图;
(3)若全校有![]() 名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列结论正确的有( )
A.公共汽年上有10位乘客,沿途5个车站,乘客下车的可能方式有![]() 种.
种.
B.两位男生和两位女生随机排成一列,则两位女生不相邻的概率是![]() ;
;
C.若随机変量![]() 服从二项分布
服从二项分布![]() ,则
,则![]() ;
;
D.已知一组数据丢失了其中一个,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数、中位数,众数依次成等差数列,则丢失数据的所有可能值的和为12.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱椎![]() 中,
中, ![]() 是棱
是棱![]() 上一点,且
上一点,且![]() ,底面
,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 为正三角形,且平面
为正三角形,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.
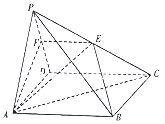
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球.
(1)求整个过程中恰好取到2个白球的概率;
(2)求取球次数的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com