练习册

  • 练习册
  • 试题
    相关习题
     0  262934  262942  262948  262952  262958  262960  262964  262970  262972  262978  262984  262988  262990  262994  263000  263002  263008  263012  263014  263018  263020  263024  263026  263028  263029  263030  263032  263033  263034  263036  263038  263042  263044  263048  263050  263054  263060  263062  263068  263072  263074  263078  263084  263090  263092  263098  263102  263104  263110  263114  263120  263128  266669 

    科目： 来源： 题型：

    【题目】进入冬天，大气流动性变差，容易形成雾握天气，从而影响空气质量．某城市环保部门试图探究车流量与空气质量的相关性，以确定是否对车辆实施限行．为此，环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表：

    (1)根据表中周一到周五的数据，求y关于x的线性回归方程。

    (2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2，则认为得到的线性回归方程是可靠的．请根据周六和周日数据，判定所得的线性回归方程是否可靠？

    注：回归方程中斜率和截距最小二乘估计公式分别为.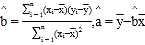

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知A、B是单位圆O上的两点（O为圆心），∠AOB=120°，点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径，则的取值范围是（ ）

    A. [，0） B. [，0] C. [，1） D. [，1]

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】数据x1，x2，x3，x4，x5的方差是2，则数据x1－1，x2－1，x3－1，x4－1，x5－1的方差是____．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知椭圆C：的右焦点为F，点A（一2，2)为椭圆C内一点。若椭圆C上存在一点P，使得｜PA｜＋｜PF｜＝8，则m的取值范围是（ ）．

    A. B. ［9，25］ C. D. ［3，5］

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，已知点，是以为底边的等腰三角形，点在直线:上．

    （1）求边上的高所在直线的方程；

    （2）求的面积．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车，等可能随机顺序前往酒店接嘉宾．某嘉宾突发奇想，设计两种乘车方案．方案一：不乘坐第一辆车，若第二辆车的车序号大于第一辆车的车序号，就乘坐此车，否则乘坐第三辆车；方案二：直接乘坐第一辆车．记方案一与方案二坐到“3号”车的概率分别为P1，P2，则（ ）

    A. P1P2＝ B. P1＝P2＝ C. P1+P2＝ D. P1＜P2

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在如图所示的四棱锥中，底面为菱形，,为正三角形.

    （1）证明:；

    （2）若，四棱锥的体积为16，求的长.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】定义在上的奇函数有最小正周期，且时，.

    （1）求在上的解析式；

    （2）判断在上的单调性，并给予证明；

    （3）当为何值时，关于方程在上有实数解？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在平面直角坐标系中，已知椭圆的离心率为，短轴长为2．

    （Ⅰ）求椭圆C的标准方程；

    （Ⅱ）设P为椭圆上顶点，点A是椭圆C上异于顶点的任意一点，直线交x轴于点M，点B与点A关于x轴对称，直线交x轴于点N．问：在y轴的正半轴上是否存在点Q，使得？若存在，求点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】进入冬天，大气流动性变差，容易形成雾握天气，从而影响空气质量．某城市环保部门试图探究车流量与空气质量的相关性，以确定是否对车辆实施限行．为此，环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表：

    (1)根据表中周一到周五的数据，求y关于x的线性回归方程。

    (2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2，则认为得到的线性回归方程是可靠的．请根据周六和周日数据，判定所得的线性回归方程是否可靠？

    注：回归方程中斜率和截距最小二乘估计公式分别为.

    查看答案和解析>>

    同步练习册答案