
科目: 来源: 题型:
【题目】在![]() 年
年![]() 月
月![]() 日,某市物价部门对本市的
日,某市物价部门对本市的![]() 家商场的某商品的一天销售量及其价格进行调查,
家商场的某商品的一天销售量及其价格进行调查,![]() 家商场的售价
家商场的售价![]() 元和销售量
元和销售量![]() 件之间的一组数据如表所示:
件之间的一组数据如表所示:
价格 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量 | 11 | 10 | 8 | 6 | 5 |
根据公式计算得相关系数![]() ,其线性回归直线方程是:
,其线性回归直线方程是:![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
参考:![]()
A.有![]() 的把握认为变量
的把握认为变量![]() 具有线性相关关系
具有线性相关关系
B.回归直线恒过定点![]()
C.![]()
D.当![]() 时,
时,![]() 的估计值为
的估计值为![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某村电费收取有以下两种方案供农户选择:
方案一:每户每月收取管理费2元,月用电量不超过30度时,每度0.5元;超过30度时,超过部分按每度0.6元收取:
方案二:不收取管理费,每度0.58元.
(1)求方案一的收费L(x)(元)与用电量x(度)间的函数关系.若老王家九月份按方案一缴费35元,问老王家该月用电多少度?
(2)老王家该月用电量在什么范围内,选择方案一比选择方案二好?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() 和
和![]() .
.
(![]() )若
)若![]() ,
, ![]() 是正方形一条边上的两个顶点,求这个正方形过顶点
是正方形一条边上的两个顶点,求这个正方形过顶点![]() 的两条边所在直线的方程;
的两条边所在直线的方程;
(![]() )若
)若![]() ,
, ![]() 是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
是正方形一条对角线上的两个顶点,求这个正方形另外一条对角线所在直线的方程及其端点的坐标.
查看答案和解析>>
科目: 来源: 题型:
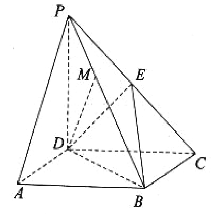
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
(1)若![]() 平面
平面![]() ,证明:
,证明:![]() ;
;
(2)在(1)的条件下,棱![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“中国大能手”是央视推出的一档大型职业技能挑战赛类节目,旨在通过该节目,在全社会传播和弘扬“劳动光荣、技能宝贵、创造伟大”的时代风尚.某公司准备派出选手代表公司参加“中国大能手”职业技能挑战赛.经过层层选拔,最后集中在甲、乙两位选手在一项关键技能的区分上,选手完成该项挑战的时间越少越好.已知这两位选手在15次挑战训练中,完成该项关键技能挑战所用的时间![]() (单位:秒)及挑战失败(用“×”表示)的情况如下表1:
(单位:秒)及挑战失败(用“×”表示)的情况如下表1:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| × | 96 | 93 | × | 92 | × | 90 | 86 | × | × | 83 | 80 | 78 | 77 | 75 |
| × | 95 | × | 93 | × | 92 | × | 88 | 83 | × | 82 | 80 | 80 | 74 | 73 |
据上表中的数据,应用统计软件得下表2:
均值(单位:秒)方差 | 方差 | 线性回归方程 | |
甲 | 85 | 50.2 |
|
乙 | 84 | 54 |
|
(1)根据上述回归方程,预测甲、乙分别在下一次完成该项关键技能挑战所用的时间;
(2)若该公司只有一个参赛名额,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,则下列结论正确的是( )
A.四面体ABCD每组对棱相互垂直
B.四面体ABCD每个面的面积相等
C.从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90°且小于180°
D.连接四面体ABCD每组对棱中点的线段相互垂直平分
查看答案和解析>>
科目: 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如表:
损坏餐椅数 | 未损坏餐椅数 | 总计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总计 | 80 | 320 | 400 |
![]() 求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
![]() 请说明是否有
请说明是否有![]() 以上的把握认为损毁餐椅数量与学习雷锋精神
以上的把握认为损毁餐椅数量与学习雷锋精神
有关?![]() 参考公式:
参考公式:![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com