【题目】已知函数.

（1）讨论函数的单调性；

（2）若，函数在区间上恰有两个零点，求的取值范围.

【题目】西北某省会城市计划新修一座城市运动公园，设计平面如图所示：其为五边形，其中三角形区域为球类活动场所；四边形为文艺活动场所，，为运动小道（不考虑宽度），，千米.

（1）求小道的长度；

（2）求球类活动场所的面积最大值.

【题目】已知直线l：与拋物线C：相切．

（1）求拋物线方程；

（2）斜率不为0的直线经过拋物线C的焦点F，交抛物线于两点A，B，拋物线C上是否存在两点D，E关于直线对称．若存在求出斜率k的取值范围；若不存在，说明理由．

【题目】电子芯片是“中国智造”的灵魂，是所有整机设备的“心脏”.某国产电子芯片公司，通过大数据分析，得到如下规律：生产一种高端芯片x（）万片，其总成本为，其中固定成本为800万元，并且每生产1万片的生产成本为200万元（总成本=固定成本+生产成本），销售收入（单位：万元）满足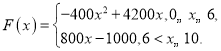假定生产的芯片都能卖掉.

（1）将利润（单位：万元）表示为产量x（单位：万片）的函数；

（2）当产量x（单位：万片）为何值时，公司所获利润最大？最大利润为多少万元？

【题目】已知点P是椭圆上的动点，、为椭圆的左、右焦点，O为坐标原点，若M是的角平分线上的一点，且F1M⊥MP，则|OM|的取值范围是( )

A．B．C．D．

【题目】(1)利用“五点法”画出函数在长度为一个周期的闭区间的简图.

列表:

作图:

(2)并说明该函数图象可由的图象经过怎么变换得到的.

(3)求函数图象的对称轴方程.

（1）求1名顾客摸球2次摸奖停止的概率；

（2）记X为1名顾客摸奖获得的奖金数额，求随机变量X的分布列和数学期望.

【题目】如图，在三棱柱中，侧面是菱形，且，平面平面，，，O为的中点．

（1）求证：

（2）求二面角的余弦值．

【题目】已知函数（为自然对数的底数，）.

（1）求函数在点处的切线方程；

（2）若对于任意，存在，使得，求的取值范围；

（3）若恒成立，求的取值范围.

【题目】《九章算术》是我国古代数学文化的优秀遗产，数学家刘徽在注解《九章算术》时，发现当圆内接正多边行的边数无限增加时，多边形的面积可无限逼近圆的面积，为此他创立了割圆术，利用割圆术，刘徽得到了圆周率精确到小数点后四位3.1416，后人称3.14为徽率，如图是利用刘徽的割圆术设计的程序框图，若结束程序时，则输出的为（ ）（，，）

A. 6 B. 12 C. 24 D. 48