
科目: 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且经过点M(1,
,且经过点M(1,![]() ).
).
(1)求椭圆C的标准方程;
(2)已知直线l不过点P(0,1),与椭圆C交于A、B两点,记直线PA、PB的斜率分别为k1、k2,且满足k1+k2=1,求证:直线l过定点,并求出该定点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】Fibonacci数列又称黄金分割数列,因为当n趋向于无穷大时,其相邻两项中的前项与后项的比值越来越接近黄金分割数![]() .已知Fibonacci数列的递推关系式为
.已知Fibonacci数列的递推关系式为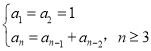 .
.
(1)证明:Fibonacci数列中任意相邻三项不可能成等比数列;
(2)Fibonacci数列{an}的偶数项依次构成一个新数列,记为{bn},证明:{bn+1-H2·bn}为等比数列.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠APC=90°,∠BPD=120°,PB=PD.
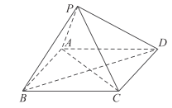
(1)求证:平面APC⊥平面BPD;
(2)若AB=2AP=2,求三棱锥C-PBD的体积.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年开始,直播答题突然就火了,在某场活动中,最终仅有23人平分100万奖金,这23人可以说是“学霸”级的大神.但随着直播答题的发展,其模式的可持续性受到了质疑,某网战随机选取500名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 180 | 140 |
认为直播答题模式不可持续 | 120 | 60 |
(1)根据表格中的数据,用独立性检验的思维方法判断是否有97.5%的把握认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的500人中,有15%曾参加答题游戏瓜分过奖金,而男性被调查者有12%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式:![]()
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
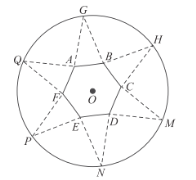
【题目】如图,圆形纸片的圆心为O,半径为5cm,该纸片上的正六边形ABCDEF的中心为O,G、H、M、N、P、Q为圆O上的点,△GAB,△HBC,△MCD,△NDE,△PEF,△QAF分别是以AB,BC,CD,DE,EF,FA为底边的等腰三角形,沿虚线剪开后,分别以AB,BC,CD,DE,EF,FA为折痕折起△GAB,△HBC,△MCD,△NDE,△PEF,△QAF,使得G、H、M、N、P、Q重合,得到六棱锥.当正六边形ABCDEF的边长变化时,所得六棱锥体积(单位:cm3)的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,则下面叙述正确的是( )
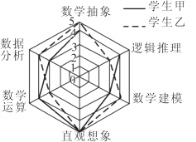
A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观想象能力指标值
C.甲的六维能力指标值整体水平优于乙的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系,将曲线![]() 上的每一个点的横坐标保持不变,纵坐标缩短为原来的
上的每一个点的横坐标保持不变,纵坐标缩短为原来的![]() ,得到曲线
,得到曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,
轴的正半轴为极轴,建立极坐标系, ![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的参数方程;
的参数方程;
(Ⅱ)过原点![]() 且关于
且关于![]() 轴对称的两条直线
轴对称的两条直线![]() 与
与![]() 分别交曲线
分别交曲线![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且点
,且点![]() 在第一象限,当四边形
在第一象限,当四边形![]() 的周长最大时,求直线
的周长最大时,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com