
科目: 来源: 题型:
【题目】2020年1月10日,引发新冠肺炎疫情的COVID-9病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为![]() ,假设每次接种后当天是否出现抗体与上次接种无关.
,假设每次接种后当天是否出现抗体与上次接种无关.
(1)求一个接种周期内出现抗体次数![]() 的分布列;
的分布列;
(2)已知每天接种一次花费100元,现有以下两种试验方案:
①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为![]() 元;
元;
②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为![]() 元.
元.
比较随机变量![]() 和
和![]() 的数学期望的大小.
的数学期望的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
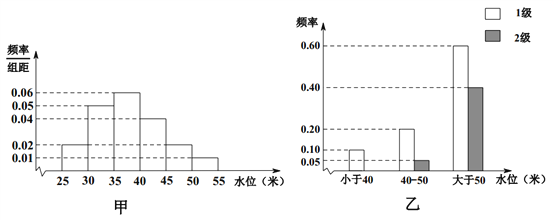
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(Ⅰ)根据列联表运用独立性检验的思想方法能否有![]() 的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数![]() 的分布列和数学期望(将频率当作概率计算).
的分布列和数学期望(将频率当作概率计算).
参考附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式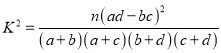 ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. “![]() 在
在![]() 处有极值”是“
处有极值”是“![]() ”的充要条件
”的充要条件
D. 命题“若函数![]() 有零点,则“
有零点,则“![]() 或
或![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com