
科目: 来源: 题型:
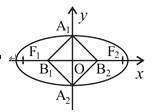
【题目】如图,已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,短轴的两端点分别为
,短轴的两端点分别为![]() ,
,![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,且四边形
,且四边形![]() 是面积为8的矩形.
是面积为8的矩形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() ,圆
,圆![]() 的方程为
的方程为![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 能否作一条直线
能否作一条直线![]() ,与点
,与点![]() 的轨迹交于
的轨迹交于![]() 两点,且点
两点,且点![]() 为线段
为线段![]() 的中点?若存在,求出直线
的中点?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市民用水拟实行阶梯水价,每人用水量中不超过![]() 立方米的部分按4元/立方米收费,超出
立方米的部分按4元/立方米收费,超出![]() 立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:
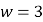
(1)如果![]() 为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,
为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米, ![]() 至少定为多少?
至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当![]() 时,估计该市居民该月的人均水费.
时,估计该市居民该月的人均水费.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知高中学生的数学成绩与物理成绩具有线性相关关系,在一次考试中某班7名学生的数学成绩与物理成绩如下表:
数学成绩 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理成绩 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)求这7名学生的数学成绩的极差和物理成绩的平均数;
(2)求物理成绩![]() 对数学成绩
对数学成绩![]() 的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
的线性回归方程;若某位学生的数学成绩为110分,试预测他的物理成绩是多少?
下列公式与数据可供参考:
用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: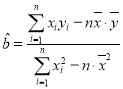 ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的个数是( )
①设某大学的女生体重![]() 与身高
与身高![]() 具有线性相关关系,根据一组样本数据
具有线性相关关系,根据一组样本数据![]() ,用最小二乘法建立的线性回归方程为
,用最小二乘法建立的线性回归方程为![]() ,则若该大学某女生身高增加
,则若该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]() ;
;
②关于![]() 的方程
的方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
,![]() 为原点,若
为原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
④已知![]() 是椭圆
是椭圆![]() 的左焦点,设动点
的左焦点,设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() ,则直线
,则直线![]() (
(![]() 为原点)的斜率的取值范围是
为原点)的斜率的取值范围是![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是2018年第一季度五省GDP情况图,则下列描述中不正确的是( )

A. 与去年同期相比2018年第一季度五个省的GDP总量均实现了增长
B. 2018年第一季度GDP增速由高到低排位第5的是浙江省
C. 2018年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D. 去年同期河南省的GDP总量不超过4000亿元
查看答案和解析>>
科目: 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为1的直线与抛物线
且斜率为1的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上异于
上异于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的准线分别交于点
的准线分别交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】[2019·清远期末]一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
有关,现收集了4组观测数据列于下表中,根据数据作出散点图如下:
温度 | 20 | 25 | 30 | 35 |
产卵数 | 5 | 20 | 100 | 325 |

(1)根据散点图判断![]() 与
与![]() 哪一个更适宜作为产卵数
哪一个更适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(数字保留2位小数);
的回归方程(数字保留2位小数);
(3)要使得产卵数不超过50,则温度控制在多少![]() 以下?(最后结果保留到整数)
以下?(最后结果保留到整数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系内,已知点![]() ,圆
,圆![]() 的方程为
的方程为![]() ,点
,点![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 能否作一条直线
能否作一条直线![]() ,与点
,与点![]() 的轨迹交于
的轨迹交于![]() 两点,且点
两点,且点![]() 为线段
为线段![]() 的中点?若存在,求出直线
的中点?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com