
科目: 来源: 题型:
【题目】已知函数h(x)=x2ex,f(x)=h(x)﹣aex(a∈R).
(Ⅰ)求函数h(x)的单调区间;
(Ⅱ)若x1,x2∈(1,2),且x1≠x2,使得f(x1)=f(x2)成立,求a的取值范围;
(Ⅲ)若函数f(x)有两个不同的极值点x1,x2,求证:f(x1)f(x2)<4e﹣2.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知极坐标系中,点![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 在曲线
在曲线![]() 上运动,以极点为坐标原点,极轴为
上运动,以极点为坐标原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为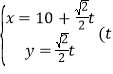 为参数
为参数![]() 。
。
(1)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(2)求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值。
的距离的最大值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 是椭圆
是椭圆![]() 上的点,且
上的点,且![]() 的面积为
的面积为![]() 。
。
(1)求椭圆![]() 的方程;
的方程;
(2)若斜率为![]() 且在
且在![]() 轴上的截距为
轴上的截距为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于两点
相交于两点![]() ,若椭圆
,若椭圆![]() 上存在点
上存在点![]() ,满足
,满足![]() ,其中
,其中![]() 是坐标原点,求
是坐标原点,求![]() 的值。
的值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x3![]() ax2﹣x+1(a∈R).
ax2﹣x+1(a∈R).
(1)当a=2时,求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当a<0时,设g(x)=f(x)+x.
①求函数g(x)的极值;
②若函数g(x)在[1,2]上的最小值是﹣9,求实数a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲,乙两人进行定点投篮活动,已知他们每投篮一次投中的概率分别是![]() 和
和![]() ,每次投篮相互独立互不影响.
,每次投篮相互独立互不影响.
(Ⅰ)甲乙各投篮一次,记“至少有一人投中”为事件A,求事件A发生的概率;
(Ⅱ)甲乙各投篮一次,记两人投中次数的和为X,求随机变量X的分布列及数学期望;
(Ⅲ)甲投篮5次,投中次数为ξ,求ξ=2的概率和随机变量ξ的数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】水果的价格会受到需求量和天气的影响.某采购员定期向某批发商购进某种水果,每箱水果的价格会在当日市场价的基础上进行优惠,购买量越大优惠幅度越大,采购员通过对以往的10组数据进行研究,发现可采用![]() 来作为价格的优惠部分
来作为价格的优惠部分![]() (单位:元/箱)与购买量
(单位:元/箱)与购买量![]() (单位:箱)之间的回归方程,整理相关数据得到下表(表中
(单位:箱)之间的回归方程,整理相关数据得到下表(表中![]() ):
):
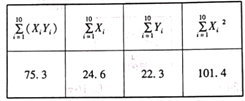
(1)根据参考数据,
①建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②若当日该种水果的市场价为200元/箱,估算购买100箱该种水果所需的金额(精确到0.1元).
(2)在样本中任取一点,若它在回归曲线上或上方,则称该点为高效点.已知这10个样本点中,高效点有4个,现从这10个点中任取3个点,设取到高效点的个数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为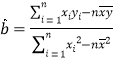 ,
,![]() ,参考数据:
,参考数据:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com