【题目】已知椭圆的离心率为，且过点.

（1）求椭圆的标准方程；

（2）若，为椭圆上不同的两点，且以为直径的圆过坐标原点.是否存在定圆与动直线相切？若存在，求出该圆的方程；若不存在，说明理由.

已知在全部300人中随机抽取1人，抽到学习积极性不高的学生的概率为.

（1）请将上面的列联表补充完整；

（2）是否有的把握认为学习积极性高与参加文体活动有关？请说明你的理由；

（3）若从不参加文体活动的同学中按照分层抽样的方法选取5人，再从所选出的5人中随机选取2人，求至少有1人学习积极性不高的概率.

附：

，其中.

【题目】《九章算术》是我国古代的数学名著，书中对几何学的研究比西方早一千多年.在该书中，将底面为直角三角形，且侧棱垂直于底面的三棱柱称为堑堵；将底面为矩形，一侧棱垂直于底面的四棱锥称为阳马；将四个面均为直角三角形的四面体称为鳖臑.如图，在堑堵中，，，鳖臑的体积为2，则阳马外接球表面积的最小值为__________．

【题目】设，是两条不重合的直线，，是两个不重合的平面，下列说法正确的是（ ）

A. 若，，，则

B. 若，，则

C. 若，，则

D. 若，，，则

已知函数在区间，内各有一个极值点．

（I）求的最大值；

（II）当时，设函数在点处的切线为，若在点处穿过函数的图象（即动点在点附近沿曲线运动，经过点时，从的一侧进入另一侧），求函数的表达式．

【题目】已知直线x＝﹣2上有一动点Q，过点Q作直线l，垂直于y轴，动点P在l1上，且满足(O为坐标原点)，记点P的轨迹为C．

（1）求曲线C的方程；

（2）已知定点M(，0)，N(，0)，点A为曲线C上一点，直线AM交曲线C于另一点B，且点A在线段MB上，直线AN交曲线C于另一点D，求△MBD的内切圆半径r的取值范围．

（1）用X表示抽取的3人中是抖音迷的员工人数，求随机变量X的分布列与数学期望；

（2）设A为事件“抽取的3人中，既有是抖音迷的员工，也有非抖音迷的员工”，求事件A发生的概率.

A.0.15B.0.21C.0.24D.0.30

【题目】如图，将边长为2的正方形沿对角线折叠，使得平面平面，又平面.

（1）若，求直线与直线所成的角；

（2）若二面角的大小为，求的长度．

【题目】“工资条里显红利，个税新政人民心”，随着2019年新年钟声的敲响，我国自1980年以来，力度最大的一次个人所得税（简称个税）改革迎来了全面实施的阶段，某从业者为了解自己在个税新政下能享受多少税收红利，绘制了他在26岁~35岁（2009年~2018年）之间各月的月平均收入(单位：千元)的散点图：

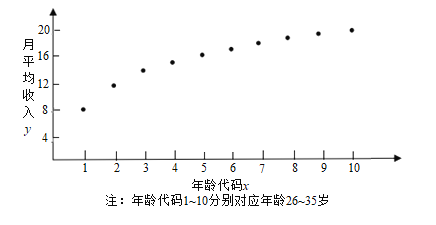
（1）由散点图知，可用回归模型拟合与的关系，试根据有关数据建立关于的回归方程；

（2）如果该从业者在个税新政下的专项附加扣除为3000元/月，试利用（1）的结果，将月平均收入为月收入，根据新旧个税政策，估计他36岁时每个月少缴交的个人所得税.

附注：

参考数据，，，，，,，其中；取，

参考公式：回归方程中斜率和截距的最小二乘估计分别为,

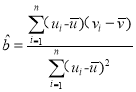新旧个税政策下每月应纳税所得额（含税）计算方法及税率表如下：