
科目: 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2
,以椭圆的2个焦点与1个短轴端点为顶点的三角形的面积为2![]() 。
。
(1)求椭圆的方程;
(2)如图,斜率为k的直线l过椭圆的右焦点F,且与椭圆交与A,B两点,以线段AB为直径的圆截直线x=1所得的弦的长度为![]() ,求直线l的方程。
,求直线l的方程。
查看答案和解析>>
科目: 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )

A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
的展开式中第5项与第7项的二项数系数相等,且展开式的各项系数之和为1024,则下列说法正确的是( )
A.展开式中奇数项的二项式系数和为256
B.展开式中第6项的系数最大
C.展开式中存在常数项
D.展开式中含![]() 项的系数为45
项的系数为45
查看答案和解析>>
科目: 来源: 题型:
【题目】口袋中放有20个球,其中白球9个、红球5个、黑球6个,现从中任取10个球,使得白球不少于![]() 个不多于7个,红球不少于2个不多于5个、黑球不多于3个的取法种数是( )
个不多于7个,红球不少于2个不多于5个、黑球不多于3个的取法种数是( )
A. 14 B. 24
C. 13 D. 36
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题正确的是( )
A.已知随机变量![]() ,若
,若![]() .则
.则![]()
B.已知分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观察值为
的观察值为![]() ,则当
,则当![]() 的值越大时,“
的值越大时,“![]() 与
与![]() 有关”的可信度越小.
有关”的可信度越小.
C.在线性回归模型中,计算其相关指数![]() ,则可以理解为:解析变量对预报变量的贡献率约为
,则可以理解为:解析变量对预报变量的贡献率约为![]()
D.若对于变量![]() 与
与![]() 的
的![]() 组统计数据的线性回归模型中,相关指数
组统计数据的线性回归模型中,相关指数![]() .又知残差平方和为
.又知残差平方和为![]() .那么
.那么![]() .(注意:
.(注意: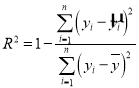 )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如表:
得分 |
|
|
|
|
|
|
|
男性 人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性 人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解”(得分不低于60分)和“不太了解”(得分低于60分)两类,完成2×2列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,现从这10人中随机抽取3人作为环保宣传队长,设3人中男性队长的人数为ξ,求ξ的分布列和期望.
附:![]()
![]() ,(n=a+b+c+d).
,(n=a+b+c+d).
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
【题目】在某次投篮测试中,有两种投篮方案:方案甲:先在A点投篮一次,以后都在B点投篮;方案乙:始终在B点投篮.每次投篮之间相互独立.某选手在A点命中的概率为![]() ,命中一次记3分,没有命中得0分;在B点命中的概率为
,命中一次记3分,没有命中得0分;在B点命中的概率为![]() ,命中一次记2分,没有命中得0分,用随机变量
,命中一次记2分,没有命中得0分,用随机变量![]() 表示该选手一次投篮测试的累计得分,如果
表示该选手一次投篮测试的累计得分,如果![]() 的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
的值不低于3分,则认为其通过测试并停止投篮,否则继续投篮,但一次测试最多投篮3次.
(1)若该选手选择方案甲,求测试结束后所得分![]() 的分布列和数学期望.
的分布列和数学期望.
(2)试问该选手选择哪种方案通过测试的可能性较大?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),点
为参数),点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)试判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(2)设直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com