
科目: 来源: 题型:
【题目】请你设计一个包装盒,如图所示,![]() 是边长为
是边长为![]() 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得![]() 四个点重合于图中的点
四个点重合于图中的点![]() ,正好形成一个正四棱柱形状的包装盒,
,正好形成一个正四棱柱形状的包装盒,![]() 在
在![]() 上,是被切去的一个等腰直角三角形斜边的两个端点,设
上,是被切去的一个等腰直角三角形斜边的两个端点,设![]() (
(![]() ).
).

(1)某广告商要求包装盒的侧面积![]()
![]() 最大,试问
最大,试问![]() 应取何值?
应取何值?
(2)某厂商要求包装盒的容积![]() 最大,试问
最大,试问![]() 应取何值?并求出此时包装盒的高与底面边长的比值.
应取何值?并求出此时包装盒的高与底面边长的比值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.

(Ⅰ)求证:![]() ;
;
(Ⅱ)是否存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前56项和为( )

A.2060B.2038C.4084D.4108
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线C1:y=![]() x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2:![]() -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
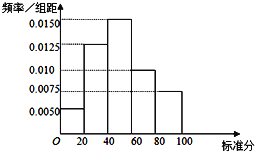
【题目】为了改善市民的生活环境,信阳市决定对信阳市的1万家中小型化工企业进行污染情况摸排,并出台相应的整治措施.通过对这些企业的排污口水质,周边空气质量等的检验,把污染情况综合折算成标准分100分,发现信阳市的这些化工企业污染情况标准分基本服从正态分布N(50,162),分值越低,说明污染越严重;如果分值在[50,60]内,可以认为该企业治污水平基本达标.
(1)如图是信阳市的某工业区所有被调查的化工企业的污染情况标准分的频率分布直方图,请计算这个工业区被调查的化工企业的污染情况标准分的平均值,并判断该工业区的化工企业的治污平均值水平是否基本达标;
(2)大量调査表明,如果污染企业继续生产,那么标准分低于18分的化工企业每月对周边造成的直接损失约为10万元,标准分在[18,34)内的化工企业每月对周边造成的直接损失约为4万元.长沙市决定关停80%的标准分低于18分的化工企业和60%的标准分在[18,34)内的化工企业,每月可减少的直接损失约有多少?
(附:若随机变量![]() ,则
,则![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两个班级(各40名学生)进行一门考试,为易于统计分析,将甲、乙两个班学生的成绩分成如下四组:![]() ,
,![]() ,
,![]() ,
,![]() ,并分别绘制了如下的频率分布直方图:
,并分别绘制了如下的频率分布直方图:
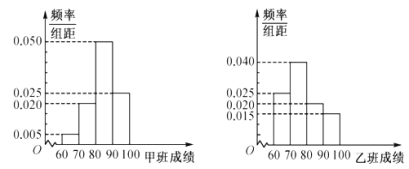
规定:成绩不低于90分的为优秀,低于90分的为不优秀.
(1)根据这次抽查的数据,填写下面的![]() 列联表:
列联表:
优秀 | 不优秀 | 合计 | |
甲班 | |||
乙班 | |||
合计 |
(2)根据(1)中的列联表,能否有![]() 的把握认为成绩是否优秀与班级有关?
的把握认为成绩是否优秀与班级有关?
附:临界值参考表与参考公式
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(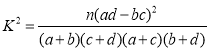 ,其中
,其中![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为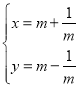 (m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(m为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线C和直线![]() 的直角坐标系方程;
的直角坐标系方程;
(2)已知![]() 直线
直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线![]() ,椭圆
,椭圆![]() 分别为椭圆的左、右焦点.
分别为椭圆的左、右焦点.
(1)当直线![]() 过右焦点
过右焦点![]() 时,求椭圆
时,求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点,且
为坐标原点,且![]() ,若点
,若点![]() 在以线段
在以线段![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB![]() 平面BEC,BE
平面BEC,BE![]() EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
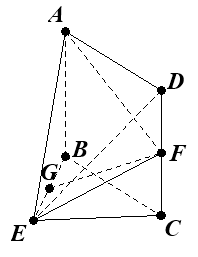
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com