【题目】已知椭圆的长轴长为4，离心率为．

（1）求椭圆的标准方程；

（2）过作动直线交椭圆于两点，为平面上一点，直线的斜率分别为，且满足，问点是否在某定直线上运动，若存在，求出该直线方程；若不存在，请说明理由．

【题目】在平面直角坐标系xOy中，已知曲线C的参数方程为为参数，以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系．

（1）求曲线C的极坐标方程；

（2）设直线l的极坐标方程为，若直线l与曲线C交于M，N两点，且，求直线l的直角坐标方程．

【题目】已知椭圆E：的离心率为，且过点

求椭圆E的方程；

设直线与椭圆E交于A、B两点，与x轴、y轴分别交于C、D两点且C、D在A、B之间或同时在A、B之外问：是否存在定值k，使得的面积与的面积总相等，若存在，求k的值，并求出实数m取值范围；若不存在，说明理由．

【题目】①；②；③（为常数）这个条件中选择个条件，补全下列试题后完成解答，设等差数列的前项和为，若数列的各项均为正整数，且满足公差，____________.

（1）求数列的通项公式；

（2）令，求数列的前项的和.

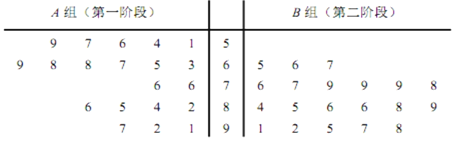
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度不要求计算出具体值，给出结论即可；

根据群众的评分将满意度从低到高分为三个等级：

假设两组群众的评价结果相互独立，由频率估计概率，求创文工作第二阶段的民众满意度等级高于第一阶段的概率；

从这40名群众中随机抽取2人，记X表示满意度等级为“非常满意”的群众人数，求X的分布列与数学期望．

【题目】如图，已知是边长为6的等边三角形，点D、E分别是边AB、AC上的点，且满足，如图，将沿DE折成四棱锥，且有平面平面BCED．

求证：平面BCED；

记的中点为M，求二面角的余弦值．

【题目】把分别写有1，2，3，4，5的五张卡片全部分给甲、乙、丙三个人，每人至少一张，且若分得的卡片超过一张，则必须是连号，那么不同的分法种数为______用数字作答．

【题目】椭圆的离心率是，过点做斜率为的直线，椭圆与直线交于两点，当直线垂直于轴时．

（Ⅰ）求椭圆的方程；

（Ⅱ）当变化时，在轴上是否存在点，使得是以为底的等腰三角形，若存在求出的取值范围，若不存在说明理由．

由此得出的正确结论是（ ）

A.有10%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖有关”

B.有10%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖无关”

C.有90%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖有关”

D.有90%的把握认为“该地中年人的低密度脂蛋白浓度与肥胖无关”

【题目】已知函数 （为常数）

（Ⅰ）若是定义域上的单调函数，求的取值范围；

（Ⅱ）若存在两个极值点，且，求的最大值．