
科目: 来源: 题型:
【题目】如果![]() 不是等差数列,但若
不是等差数列,但若![]() ,使得
,使得![]() ,那么称
,那么称![]() 为“局部等差”数列.已知数列
为“局部等差”数列.已知数列![]() 的项数为4,记事件
的项数为4,记事件![]() :集合
:集合![]() ,事件
,事件![]() :
:![]() 为“局部等差”数列,则条件概率
为“局部等差”数列,则条件概率![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】小王、小李在两次数学考试中答对题数如下表表示:
题型 答对 题数 姓名 | 期中考试 | 期末考试 | ||||
填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | 填空题 (每题3分) | 选择题 每题3分) | 解答题 (每题8分) | |
小王 | 10 | 3 | 2 | 11 | 4 | 4 |
小李 | 9 | 5 | 3 | 7 | 3 | 3 |
(1)用矩阵表示小王和小李期中考试答对题数、期末考试答对题数、每种题型的分值;
(2)用矩阵运算表示他们在两次考试中各题型答对题总数;
(3)用矩阵计算小王、小李两次考试各题型平均答对题数;
(4)用矩阵计算他们期中、期末的成绩;
(5)如果期中考试成绩占40%,期末考试成绩占60%,用矩阵求两同学的总评成绩.
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
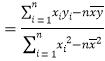 ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知如图1直角梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将梯形
将梯形![]() 折起(如图2),使平面
折起(如图2),使平面![]() 平面
平面![]() .
.
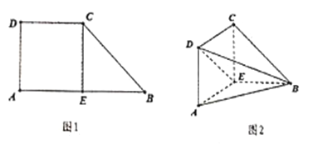
(1)证明![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国全力抗击“新冠疫情”对全球做出了巨大贡献,广大中小学生在这场“战疫”中也通过各种方式作出了贡献.某校团委准备组织一次“网上战疫”的宣传活动,活动包含4项子活动.现随机抽取了5个班级中的25名同学进行关于活动方案的问卷调查,其中关于4项子活动的赞同情况统计如下:
班级代码 | A | B | C | D | E | 合计 |
4项子活动全部赞同的人数 | 3 | 4 | 8 | 3 | 2 | 20 |
4项子活动不全部赞同的人数 | 1 | 1 | 0 | 2 | 1 | 5 |
合计问卷调查人数 | 4 | 5 | 8 | 5 | 3 | 25 |
现欲针对4项子活动的活动内容作进一步采访调研,每项子活动采访1名学生.
(1)若每项子活动都从这25名同学中随机选取1人采访,求4次采访中恰有1次采访的学生对“4项子活动不全部赞同”的概率;
(2)若从A班和E班的被问卷调查者中各随机选取2人作为采访调研的对象,记选取的4人中“4项子活动全部赞同”的人数为X,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com