
科目: 来源: 题型:
【题目】已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且
,且![]() 时
时![]() ,甲,乙,丙,丁四位同学有下列结论:
,甲,乙,丙,丁四位同学有下列结论:
甲:![]() ;
;
乙:函数![]() 在
在![]() 上是增函数;
上是增函数;
丙:函数![]() 关于直线
关于直线![]() 对称;
对称;
丁:若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在
在![]() 上所有根之和为
上所有根之和为![]() 其中正确的是( ).
其中正确的是( ).
A. 甲,乙,丁 B. 乙,丙 C. 甲,乙,丙 D. 甲,丁
查看答案和解析>>
科目: 来源: 题型:
【题目】函数![]() (a为常数,且
(a为常数,且![]() )在
)在![]() 处取得极值.
处取得极值.
(1)求实数a的值,并求![]() 的单调区间;
的单调区间;
(2)关于x的方程![]() 在
在![]() 上恰有1个实数根,求实数b的取值范围;
上恰有1个实数根,求实数b的取值范围;
(3)求证:当![]() 时,
时,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?
查看答案和解析>>
科目: 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年高考总成绩由语数外三门统考科目和物理、化学等六门选考科目组成,将每门选考科目的考生原始成绩从高到低划分为![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到
共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩
八个分数区间,得到考生的等级成绩.某市高一学生共6000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩![]() 大致服从正态分布
大致服从正态分布![]() .
.
(1)求该市化学原始成绩在区间![]() 的人数;
的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间![]() 的人数,求
的人数,求![]() .
.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】平面上有12个点且任意三点不共线.以其中任意一点为始点、另一点为终点作向量且作出所有的向量,其中,三边向量的和为零向量的三角形称为“零三角形”.求以这12个点为顶点的零三角形个数的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】“十三五”规划确定了到2020年消除贫困的宏伟目标,打响了精准扶贫的攻坚战,为完成脱贫任务,某单位在甲地成立了一家医疗器械公司吸纳附近贫困村民就工,已知该公司生产某种型号医疗器械的月固定成本为20万元,每生产1千件需另投入5.4万元,设该公司一月内生产该型号医疗器械x千件且能全部销售完,每千件的销售收入为![]() 万元,已知
万元,已知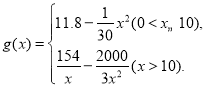
(1)请写出月利润y(万元)关于月产量x(千件)的函数解析式;
(2)月产量为多少千件时,该公司在这一型号医疗器械的生产中所获月利润最大?并求出最大月利润(精确到0.1万元).
查看答案和解析>>
科目: 来源: 题型:
【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设![]() 分别表示5名学生分配到王城公园和牡丹公园的人数,记
分别表示5名学生分配到王城公园和牡丹公园的人数,记![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 的极坐标程是
的极坐标程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程
的参数方程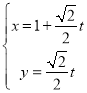 ,(
,(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为曲线
为曲线![]() 上的动点,求三角形
上的动点,求三角形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com