
科目: 来源: 题型:
【题目】经观测,某昆虫的产卵数![]() 与温度
与温度![]() 有关,现将收集到的温度
有关,现将收集到的温度![]() 和产卵数
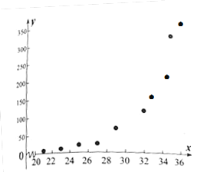
和产卵数![]() 的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
的10组观测数据作了初步处理,得到如图的散点图及一些统计量表.
|
|
|
|
|
|
275 | 731.1 | 21.7 | 150 | 2368.36 | 30 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() ,
,![]() 与
与![]() 哪一个适宜作为
哪一个适宜作为![]() 与
与![]() 之间的回归方程模型?(给出判断即可,不必说明理由)
之间的回归方程模型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据.
①试求![]() 关于
关于![]() 回归方程;
回归方程;
②已知用人工培养该昆虫的成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() ,当温度
,当温度![]() (
(![]() 取整数)为何值时,培养成本的预报值最小?
取整数)为何值时,培养成本的预报值最小?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为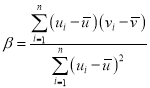 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
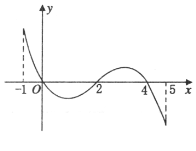
的定义域为[-1,5],部分对应值如下表,![]() 的导函数
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题正确的是( )
的命题正确的是( )
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
A.函数![]() 的极大值点为0,4;
的极大值点为0,4;
B.函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
C.如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4;
的最大值为4;
D.函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.
查看答案和解析>>
科目: 来源: 题型:
【题目】求最小的正整数![]() ,使得存在一个
,使得存在一个![]() 的数阵满足如下条件: (1)每一个数均属于集合
的数阵满足如下条件: (1)每一个数均属于集合![]() ; (2)记
; (2)记![]() 为数阵中第
为数阵中第![]() 行中的数组成的集合,
行中的数组成的集合, ![]() 为第
为第![]() 列中的数组成的集合
列中的数组成的集合![]() ,则
,则![]() ,
,![]() 是4026个不同的集合.
是4026个不同的集合.
查看答案和解析>>
科目: 来源: 题型:
【题目】圆周上有![]() 个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数
个白点,先将其中一个染为黑色(称为第一次染色),对任何正整数![]() ,第
,第![]() 次染色后按逆时针方向间隔
次染色后按逆时针方向间隔![]() 个点将下个点染成与原来颜色相反的颜色(称为第
个点将下个点染成与原来颜色相反的颜色(称为第![]() 次染色).
次染色).
(1)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为白色?
个点均为白色?
(2)对给定正整数![]() ,是否存在正整数
,是否存在正整数![]() ,使
,使![]() 次染色后
次染色后![]() 个点均为黑色?
个点均为黑色?
查看答案和解析>>
科目: 来源: 题型:
【题目】有2013支球队进行气次年度超级足球循环赛,每两支球队均恰比赛场,每场比赛胜者得3分,负者得0分,平局各得1分.比赛结束后,甲把他所在球队的总分告诉了乙,乙马上知道了甲所在球队在整个比赛中的胜负场数.试问:甲所在球队在这次比赛中所得的总分是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
平面直角坐标系![]() 中,射线
中,射线![]() :
:![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() ;以原点为极点,
;以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.曲线
轴的非负半轴为极轴建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出射线![]() 的极坐标方程以及曲线
的极坐标方程以及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)已知射线![]() 与
与![]() 交于
交于![]() ,
,![]() ,与
,与![]() 交于
交于![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】给出以下四个说法,其中正确的说法是( )
A.残差点分布的带状区域的宽度越窄相关指数越小;
B.在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
C.在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
D.对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的折线图为某小区小型超市今年1月份到5月份的营业额和支出数据(利润=营业额-支出),根据折线图,下列说法正确的是( )

A.该超市这五个月中的营业额一直在增长;
B.该超市这五个月的利润一直在增长;
C.该超市这五个月中五月份的利润最高;
D.该超市这五个月中的营业额和支出呈正相关.
查看答案和解析>>
科目: 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com