【题目】函数，关于的方程恰有四个不同的实数解，则正数的取值范围为______.

A.18B.24C.30D.36

【题目】已知函数，则以下结论正确的是（ ）

A.函数的单调减区间是

B.函数有且只有1个零点

C.存在正实数，使得成立

D.对任意两个正实数，，且，若则

【题目】若无穷数列满足：，当，时．

其中表示，，，中的最大项，有以下结论：

若数列是常数列，则

若数列是公差的等差数列，则；

若数列是公比为q的等比数列，则

则其中正确的结论是______写出所有正确结论的序号

【题目】已知函数（为自然对数的底数）.

（1）讨论函数的单调性；

（2）当时，恒成立，求整数的最大值.

注：

（1）从该公司2014-2018年的相关数据中任意选取3年的数据，求这3年中至少有2年生产部门考核优秀的概率.

（2）利用上表中五年的数据求出年利润（百万元）关于年生产台数（万台）的回归直线方程是 ①.现该公司计划从2019年开始转型，并决定2019年只生产该产品1万台，且预计2019年可获利32（百万元）；但生产部门发现，若用预计的2019年的数据与2014-2018年中考核优秀年份的数据重新建立回归方程，只有当重新估算的，的值（精确到0.01），相对于①中，的值的误差的绝对值都不超过时，2019年该产品返修率才可低于千分之一.若生产部门希望2019年考核优秀，能否同意2019年只生产该产品1万台？请说明理由.

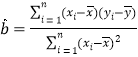
（参考公式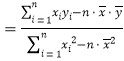：， ，，相对的误差为.）

【题目】某歌舞团有名演员，他们编排了一些节目，每个节目都由四名演员同台表演．在一次演出中，他们发现：能适当安排若干个节目，使团中每两名演员都恰有一次在这次演出中同台表演。求的最小值。

【题目】在某次会操活动中，领操员让编号为的名学生排成一个圆形阵，做循环报数，领操员一一记录报数者的编号，并要求报l、2的学生出列，报3的学生留在队列中，并将编号改为此次循环报数中三名学生的编号之和．一直循环报数下去．当操场上剩余的学生人数不超过两名时，报数活动结束．领操员记录最后留在操场的学生编号（例如，编号为的九名学生排成一个圆形阵，报数结束后，只有原始编号为9的学生留在操场，此时，他的编号为45，领操员记录下来的数据分别为l，2，3，4，5，6，7，8，9，6，15，24，45）．已知共有2011名学生参加会操．

（1）最后留在场内的学生最初的编号是几号?

（2）求领操员记录下的编号之和．

【题目】在如图所示的几何体中，四边形是正方形，四边形是梯形，，平面，且．

（1）求证：平面；

（2）求钝二面角的大小．