
科目: 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
科目: 来源: 题型:
【题目】宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入![]() ,
,![]() ,则输出的
,则输出的![]() 等于( )
等于( )
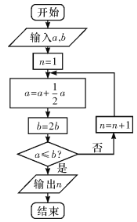
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,满足Sn=2an-1(n∈N*),数列{bn}满足nbn+1-(n+1)bn=n(n+1)(n∈N*),且b1=1.
(1)证明数列{![]() }为等差数列,并求数列{an}和{bn}的通项公式;
}为等差数列,并求数列{an}和{bn}的通项公式;
(2)若cn=(-1)n-1![]() ,求数列{cn}的前n项和T2n;
,求数列{cn}的前n项和T2n;
(3)若dn=an![]() ,数列{dn}的前n项和为Dn,对任意的n∈N*,都有Dn≤nSn-a,求实数a的取值范围.
,数列{dn}的前n项和为Dn,对任意的n∈N*,都有Dn≤nSn-a,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,底面△ABC是直角三角形,AC=BC=AA1=2,D为侧棱AA1的中点.
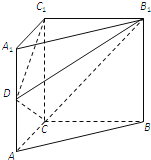
(1)求异面直线DC1,B1C所成角的余弦值;
(2)求二面角B1-DC-C1的平面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法错误的是( )
A. 在回归模型中,预报变量![]() 的值不能由解释变量
的值不能由解释变量![]() 唯一确定
唯一确定
B. 若变量![]() ,
,![]() 满足关系
满足关系![]() ,且变量
,且变量![]() 与
与![]() 正相关,则
正相关,则![]() 与
与![]() 也正相关
也正相关
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】一位幼儿园老师给班上k(k≥3)个小朋友分糖果.她发现糖果盒中原有糖果数为a0,就先从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的![]() 分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
(1)当k=3,a0=12时,分别求a1,a2,a3;
(2)请用an-1表示an;令bn=(n+1)an,求数列{bn}的通项公式;
(3)是否存在正整数k(k≥3)和非负整数a0,使得数列{an}(n≤k)成等差数列,如果存在,请求出所有的k和a0,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 为
为![]() 的焦点.
的焦点.
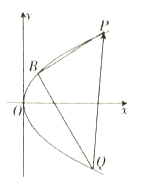
(1)若![]() ,
,![]() 是
是![]() 上的两点,证明:
上的两点,证明:![]() ,
,![]() ,
,![]() 依次成等比数列.
依次成等比数列.
(2)过![]() 作两条互相垂直的直线与
作两条互相垂直的直线与![]() 的另一个交点分别交于
的另一个交点分别交于![]() ,
,![]() (
(![]() 在
在![]() 的上方),求向量
的上方),求向量![]() 在
在![]() 轴正方向上的投影的取值范围.
轴正方向上的投影的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某小学举办“父母养育我,我报父母恩”的活动,对六个年级(一年级到六年级的年级代码分别为1,2…,6)的学生给父母洗脚的百分比y%进行了调查统计,绘制得到下面的散点图.
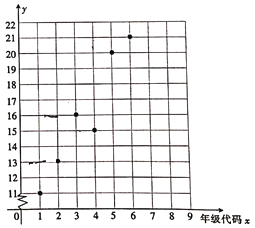
(1)由散点图看出,可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)建立y关于x的回归方程,并据此预计该校学生升入中学的第一年(年级代码为7)给父母洗脚的百分比.
附注:参考数据:![]()
参考公式:相关系数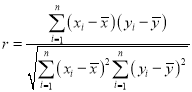 ,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程
,若r>0.95,则y与x的线性相关程度相当高,可用线性回归模型拟合y与x的关系.回归方程![]() 中斜率与截距的最小二乘估计公式分别为
中斜率与截距的最小二乘估计公式分别为![]() =
=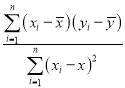 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com