
科目: 来源: 题型:
【题目】已知椭圆![]() ,抛物线
,抛物线![]() 焦点均在x轴上,
焦点均在x轴上,![]() 的中心和
的中心和![]() 顶点均在原点O,从每条曲线上各取两个点,将其坐标记录于表中,则
顶点均在原点O,从每条曲线上各取两个点,将其坐标记录于表中,则![]() 的左焦点到
的左焦点到![]() 的准线之间的距离为( )
的准线之间的距离为( )
| 3 | -2 | 4 |
|
|
| 0 | -4 |
|
A.![]() B.
B.![]() C.1D.2
C.1D.2
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学在全校范围内举办了一场“中国诗词大会”的比赛,规定初赛测试成绩不小于160分的学生进入决赛阶段比赛.现有200名学生参加测试,并将所有测试成绩统计如下表:
分数段 | 频数 | 频率 |
| 6 | 0.03 |
|
| 0.38 |
| 100 | 0.5 |
|
|
|
| 6 | 0.03 |
合计 | 200 | 1 |
(1)计算![]() 的值;
的值;
(2)现利用分层抽样的方法从进入决赛的学生中选择6人,再从选出的6人中选2人做进一步的研究,求选择的2人中至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,边长为4的正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
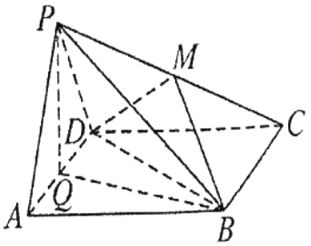
(1)求证:PA//平面MBD.
(2)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
(I)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(II)求![]() 关于
关于![]() 的线性回归方程;若该设备的价格是每台
的线性回归方程;若该设备的价格是每台![]() 万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
万元,你认为应该使用满五年换一次设备,还是应该使用满八年换一次设备?并说明理由.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: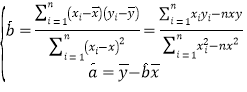
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,
,![]() 单调递增,
单调递增,![]() ,若对任意
,若对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“追逐函数”.若
上的“追逐函数”.若![]() ,则下列四个命题:①
,则下列四个命题:①![]() 是
是![]() 在
在![]() 上的“追逐函数”;②若
上的“追逐函数”;②若![]() 是
是![]() 在
在![]() 上的“追逐函数”,则
上的“追逐函数”,则![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函数”;④当
上的“追逐函数”;④当![]() 时,存在
时,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函数”.其中正确命题的个数为( )
上的“追逐函数”.其中正确命题的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设动直线![]() :
:![]() 分别与曲线
分别与曲线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 取最大值,并求
取最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com