【题目】下图1，是某设计员为一种商品设计的平面logo样式.主体是由内而外的三个正方形构成.该图的设计构思如图2,中间正方形的四个顶点,分别在最外围正方形ABCD的边上,且分所在边为a，b两段.设中间阴影部分的面积为，最内正方形的面积为.当，且取最大值时，定型该logo的最终样式，则此时a，b的取值分别为_____________.

方式一：周一到周五每天培训1小时，周日测试

方式二：周六一天培训4小时，周日测试

公司有多个班组，每个班组60人，现任选两组记为甲组、乙组先培训；甲组选方式一，乙组选方式二，并记录每周培训后测试达标的人数如表：

用方式一与方式二进行培训，分别估计员工受训的平均时间精确到，并据此判断哪种培训方式效率更高？

在甲乙两组中，从第三周培训后达标的员工中采用分层抽样的方法抽取6人，再从这6人中随机抽取2人，求这2人中至少有1人来自甲组的概率．

【题目】关于函数，.有下列命题：

①对,恒有成立.

②,使得成立.

③“若,则有且.”的否命题.

④“若且,则有.”的逆否命题.

其中，真命题有_____________.（只需填序号）

在平面直角坐标系中，将曲线向左平移2个单位，再将得到的曲线上的每一个点的横坐标保持不变，纵坐标缩短为原来的，得到曲线，以坐标原点为极点，轴的正半轴为极轴，建立极坐标系，的极坐标方程为．

（1）求曲线的参数方程；

（2）已知点在第一象限，四边形是曲线的内接矩形，求内接矩形周长的最大值，并求周长最大时点的坐标．

【题目】已知椭圆C：（a＞b＞0）的离心率为且经过点P（2，）．

（1）求椭圆C的方程；

（2）若椭圆C的左右顶点分别为A，B，过点A斜率为k（k≠0）的直线l交椭圆C于点D，交y轴于点E．是否存在定点Q，对于任意的k（k≠0）都有BD⊥EQ，若存在，求△AQD的面积的最大值；若不存在，说明理由．

【题目】已知函数

（1）若曲线在点处的切线与直线垂直，求函数的极值；

（2）设函数.当=时，若区间[1，e]上存在x0，使得，求实数的取值范围．（为自然对数底数）

【题目】已知，分别为椭圆的左、右焦点，点在椭圆上，且轴，的周长为6.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过点的直线与椭圆交于，两点，设为坐标原点，是否存在常数，使得恒成立？请说明理由.

【题目】△ABC的内角A，B，C的对边分别为a，b，c，且（b+c）tanC＝﹣ctanA．

（1）求A；

（2）若b，c＝2，点D在BC边上，且AD＝BD，求AD的长．

【题目】经过多年的努力，炎陵黄桃在国内乃至国际上逐渐打开了销路，成为炎陵部分农民脱贫致富的好产品.为了更好地销售，现从某村的黄桃树上随机摘下了100个黄桃进行测重，其质量分布在区间内（单位：克），统计质量的数据作出其频率分布直方图如图所示：

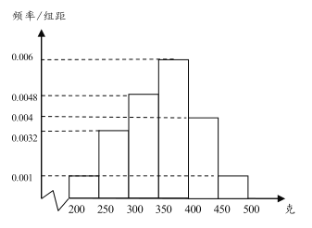
（1）按分层抽样的方法从质量落在，的黄桃中随机抽取5个，再从这5个黄桃中随机抽2个，求这2个黄桃质量至少有一个不小于400克的概率；

（2）以各组数据的中间数值代表这组数据的平均水平，以频率代表概率，已知该村的黄桃树上大约还有100000个黄桃待出售，某电商提出两种收购方案：

A.所有黄桃均以20元/千克收购；

B.低于350克的黄桃以5元/个收购，高于或等于350克的以9元/个收购.

请你通过计算为该村选择收益最好的方案.

（参考数据：）

（1）求数列{an}的通项；

（2）求数列{an}的前n项和为Sn．