（1）按分层抽样的方法从质量在，的脐橙中随机抽取5个，再从这5个脐橙中随机抽取2个，求这2个脐橙质量至少有一个不小于400克的概率；

（2）以各组数据的中间数值代替这组数据的平均值，以频率代替概率，已知该村的脐橙种植地上大约还有100000个脐橙待出售，某电商提出两种收购方案：

A.所有脐橙均以7元/千克收购；

B.低于350克的脐橙以2元/个收购，其余的以3元/个收购.

请你通过计算为该村选择收益较好的方案.

【题目】有形状和大小完全相同的小球装在三个盒子里，每个盒子装个.其中第一个盒子中有个球标有字母，有个球标有字母;第二个盒子中有个红球和个白球;第三个盒子中有个红球和个白球.现按如下规则进行试验:先在第一个盒子中随机抽取一个球，若取得字母的球，则在第二个盒子中任取一球;若取得字母的球，则在第三个盒子中任取一球.

（I）若第二次取出的是红球，则称试验成功，求试验成功的概率;

（II）若第二次在第二个盒子中取出红球，则得奖金元，取出白球则得奖金元.若第二次在第三个盒子中取出红球，则得奖金元，取出白球则得奖金元.求某人在一次试验中，所得奖金的分布列和期望.

【题目】已知定点，定直线，动圆经过点且与直线相切.

（I）求动圆圆心的轨迹方程；

（II）设点为曲线上不同的两点，且，过两点分别作曲线的两条切线，且二者相交于点，求面积的最小值.

【题目】某班进行了次数学测试，其中甲、乙两人的成绩统计情况如茎叶图所示：

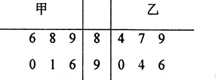
（I）该班数学老师决定从甲、乙两人中选派一人去参加数学比赛，你认为谁去更合适？并说明理由；

（II）从甲的成绩中人去两次作进一步的分析，在抽取的两次成绩中，求至少有一次成绩在之间的概率.

【题目】在直角坐标系中，曲线的参数方程为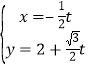(为参数)，以原点为极点，以轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为，

(Ⅰ)求曲线的普通方程和曲线的直角坐标方程；

(Ⅱ)设点，曲线与曲线交于两点，求的值．

【题目】已知正方体的棱长为，点E，F，G分别为棱AB，，的中点，下列结论中，正确结论的序号是___________.

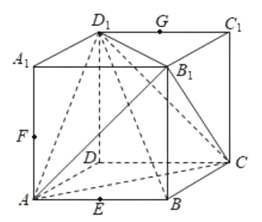
①过E，F，G三点作正方体的截面，所得截面为正六边形；

②平面EFG；

③平面；

④异面直线EF与所成角的正切值为；

⑤四面体的体积等于.

【题目】已知，函数有两个零点．

(Ⅰ)求实数的取值范围；

(Ⅱ)证明：．

【题目】为发挥体育在核心素养时代的独特育人价值，越来越多的中学已将某些体育项目纳入到学生的必修课程，甚至关系到是否能拿到毕业证.某中学计划在高一年级开设游泳课程，为了解学生对游泳的兴趣，某数学研究性学习小组随机从该校高一年级学生中抽取了100人进行调查，其中男生60人，且抽取的男生中对游泳有兴趣的占，而抽取的女生中有15人表示对游泳没有兴趣.

（1）试完成下面的列联表，并判断能否有的把握认为“对游泳是否有兴趣与性别有关”？

（2）已知在被抽取的女生中有6名高一（1）班的学生，其中3名对游泳有兴趣，现在从这6名学生中随机抽取3人，求至少有2人对游泳有兴趣的概率.

（3）该研究性学习小组在调查中发现，对游泳有兴趣的学生中有部分曾在市级和市级以上游泳比赛中获奖，如下表所示.若从高一（8）班和高一（9）班获奖学生中各随机选取2人进行跟踪调查，记选中的4人中市级以上游泳比赛获奖的人数为，求随机变量的分布列及数学期望.

.

【题目】已知函数（）．

（1）若不等式的解集为，求的取值范围；

（2）当时，解不等式；

（3）若不等式的解集为，若，求的取值范围．

【题目】圆与轴交于、两点（点在点的左侧），、是分别过、点的圆的切线，过此圆上的另一个点（点是圆上任一不与、重合的动点）作此圆的切线，分别交、于、两点，且、两直线交于点．

（）设切点坐标为，求证：切线的方程为．

（）设点坐标为，试写出与的关系表达式（写出详细推理与计算过程）．