
科目: 来源: 题型:
【题目】已知动圆M经过点F(1,0),且与直线l:x=﹣1相切,动圆圆心M的轨迹记为曲线C
(1)求曲线C的轨迹方程
(2)若点P在y轴左侧(不含y轴)一点,曲线C上存在不同的两点A、B,满足PA,PB的中点都在曲线C上,设AB中点为E,证明:PE垂直于y轴.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆![]() ,
, ![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与
过原点且与![]() 的准线相切.
的准线相切.
(Ⅰ) 求![]() 的方程;
的方程;
(Ⅱ) 点![]() ,点
,点![]() (与
(与![]() 不重合)在直线
不重合)在直线![]() 上运动,过点
上运动,过点![]() 作
作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() .求证:
.求证: ![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目: 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为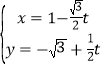 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】“新车嗨翻天!首付3000元起开新车”这就是毛豆新车网打出来的广告语.某人看到广告,兴奋不已,计划于2019年1月在该网站购买一辆某品牌汽车,他从当地了解到近五个月该品牌汽车实际销量如表:
月份 | 2018.08 | 2018.09 | 2018.10 | 2018.11 | 2018.12 |
月份编号t | 1 | 2 | 3 | 4 | 5 |
销量y(万辆) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析,可用线性回归模型拟合当地该品牌汽车实际销量y(万辆)与月份编号t之间的相关关系.请用最小二乘法求y关于t的线性回归方程![]() ,并估计2019年1月份该品牌汽车的销量:
,并估计2019年1月份该品牌汽车的销量:
(2)为了增加销量,厂家和毛豆新车网联合推出对购该品牌车进行补贴.已知某地拟购买该品牌汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值 区间(万元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) | [6,7) |
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
将频率视为概率,现用随机抽样方法从该地区拟购买该品牌汽车的所有消费者中随机抽取3人,记被抽取3人中对补贴金额的心理预期值不低于3万元的人数为ξ,求ξ的分布列及数学期望E(ξ)
参考公式及数据:①回归方程![]() ,其中
,其中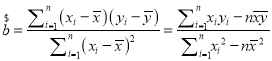 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校在2018年的自主招生考试成绩中随机抽取100名学生的笔试成绩,折合成标准分后,最高分是10分.按成绩共分成五组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),得到的频率分布直方图如图所示:
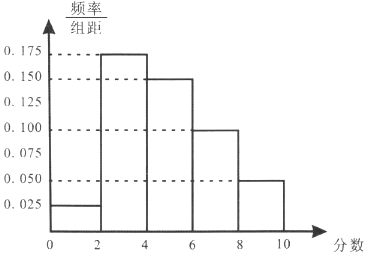
(1)分别求第三,四,五组的频率;
(2)该学校在第三,四,五组中用分层抽样的方法抽取6名同学.
①已知甲同学和乙同学均在第三组,求甲、乙同时被选中的概率
②若在这6名同学中随机抽取2名,设第4组中有X名同学,求X的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.

(1)求这200名学生每周阅读时间的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中间值代表);
(同一组中的数据用该组区间的中间值代表);
(2)由直方图可以认为,目前该校学生每周的阅读时间![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)一般正态分布的概率都可以转化为标准正态分布的概率进行计算:若![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .利用直方图得到的正态分布,求
.利用直方图得到的正态分布,求![]() .
.
(ii)从该高校的学生中随机抽取20名,记![]() 表示这20名学生中每周阅读时间超过10小时的人数,求
表示这20名学生中每周阅读时间超过10小时的人数,求![]() (结果精确到0.0001)以及
(结果精确到0.0001)以及![]() 的数学期望.
的数学期望.
参考数据:![]() ,
,![]() .若
.若![]() ,则
,则![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】设命题p:实数m满足使方程![]() 1,其中a>0为双曲线:命题q:实数m满足
1,其中a>0为双曲线:命题q:实数m满足![]() .
.
(1)若a=1且p∧q为真,求实数m的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】有下列说法:
①一支田径队有男女运动员98人,其中男运动员有56人.按男、女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是12人;
②在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4,则X在(0,2)内取值的概率为0.8.
③废品率x%和每吨生铁成本y(元)之间的回归直线方程为![]() 2x+256,这表明废品率每增加1%,生铁成本大约增加258元;
2x+256,这表明废品率每增加1%,生铁成本大约增加258元;
④为了检验某种血清预防感冒的作用,把500名未使用血清和使用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防作用”,利用2×2列联表计算得K2的观测值k≈3.918,经查对临界值表知P(K2≥3841)≈0.05,由此,得出以下判断:在犯错误的概率不超过0.05的前提下认为“这种血清能起到预防的作用”,
正确的有( )
A.①②④B.①②③C.①③D.③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,椭圆![]() ,抛物线
,抛物线![]() ,过
,过![]() 上一点
上一点![]() 异于原点
异于原点![]() 作
作![]() 的切线l交
的切线l交![]() 于A,B两点,切线l交x轴于点Q.
于A,B两点,切线l交x轴于点Q.
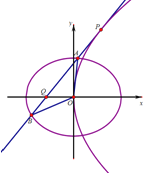
![]() 若点P的横坐标为1,且
若点P的横坐标为1,且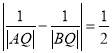 ,求p的值.
,求p的值.
![]() 求
求![]() 的面积的最大值,并求证当
的面积的最大值,并求证当![]() 面积取最大值时,对任意的
面积取最大值时,对任意的![]() ,直线l均与一个定椭圆相切.
,直线l均与一个定椭圆相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com