
科目: 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某乡镇政府为了解决农村教师的住房问题,计划征用一块土地盖一幢建筑总面积为10000![]() 公寓楼(每层的建筑面积相同).已知士地的征用费为
公寓楼(每层的建筑面积相同).已知士地的征用费为![]() ,土地的征用面积为第一层的
,土地的征用面积为第一层的![]() 倍,经工程技术人员核算,第一层建筑费用为
倍,经工程技术人员核算,第一层建筑费用为![]() ,以后每增高一层,其建筑费用就增加
,以后每增高一层,其建筑费用就增加![]() ,设这幢公寓楼高层数为n,总费用为
,设这幢公寓楼高层数为n,总费用为![]() 万元.(总费用为建筑费用和征地费用之和)
万元.(总费用为建筑费用和征地费用之和)
(1)若总费用不超过835万元,求这幢公寓楼最高有多少层数?
(2)试设计这幢公寓的楼层数,使总费用最少,并求出最少费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法正确的是( )
A.命题“若![]() .则a,b中至少有一个不小于1”的逆命题是一个真命题
.则a,b中至少有一个不小于1”的逆命题是一个真命题
B.命题“负数的平方是正数”是特称命题
C.命题“设a,![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题
”是一个真命题
D.常数数列既是等差数列也是等比数列
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某人工景观湖外围有两条相互垂直的直线型公路ll,l2,且ll和l2交于点O.为了方便游客游览,计划修建一条连接公路与景观湖的直线型公路AB.景观湖的轮廓可以近似看成一个圆心为O,半径为2百米的圆,且公路AB与圆O相切,圆心O到ll,l2的距离均为5百米,设OAB=![]() ,AB长为L百米.
,AB长为L百米.
(1)求L关于![]() 的函数解析式;
的函数解析式;
(2)当![]() 为何值时,公路AB的长度最短?
为何值时,公路AB的长度最短?

查看答案和解析>>
科目: 来源: 题型:
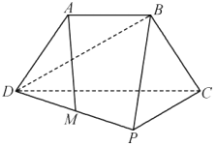
【题目】如图,三角形PCD所在的平面与等腰梯形ABCD所在的平面垂直,AB=AD=![]() CD,AB∥CD,CP⊥CD,M为PD的中点.
CD,AB∥CD,CP⊥CD,M为PD的中点.
(1)求证:AM∥平面PBC;
(2)求证:BD⊥平面PBC.
查看答案和解析>>
科目: 来源: 题型:
【题目】制订投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目.根据预测,甲、乙项目可能的最大盈利分别为![]() 和
和![]() ,可能的最大亏损率分别为
,可能的最大亏损率分别为![]() 和
和![]() .投资人计划投资金额不超过
.投资人计划投资金额不超过![]() 亿元,要求确保可能的资金亏损不超过
亿元,要求确保可能的资金亏损不超过![]() 亿元,问投资人对甲、乙两个项目各投资多少亿元,才能使可能的盈利最大?
亿元,问投资人对甲、乙两个项目各投资多少亿元,才能使可能的盈利最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】在边长为8的正方形ABCD中,M是BC的中点,N是AD边上的一点,且DN=3NA,若对于常数m,在正方形ABCD的边上恰有6个不同的点P,使![]() ,则实数m的取值范围是_______.
,则实数m的取值范围是_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆E:![]() 1(a>0)的中心为原点O,左、右焦点分别为F1、F2,离心率为
1(a>0)的中心为原点O,左、右焦点分别为F1、F2,离心率为![]() ,点P是直线x
,点P是直线x![]() 上任意一点,点Q在椭圆E上,且满足
上任意一点,点Q在椭圆E上,且满足![]() 0.
0.
(1)试求出实数a;
(2)设直线PQ与直线OQ的斜率分别为k1与k2,求积k1k2的值;
(3)若点P的纵坐标为1,过点P作动直线l与椭圆交于不同的两点M、N,在线段MN上取异于点M、N的点H,满足![]() ,证明点H恒在一条定直线上.
,证明点H恒在一条定直线上.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,动点M在边DC上(不同于D点),P为边AB上任意一点,沿AM将△ADM翻折成△AD'M,当平面AD'M垂直于平面ABC时,线段PD'长度的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com